5.3 データ構造
5.3.1 多次元配列
-
まず簡単なところで、次のような問題が与えられた時、どのようなデータ構造が考えられどんなデータ型で実現できるか、考えてみよう。
例5−13
考え方:
-
簡単にするため便宜上sinのグラフを描く際に、上から下方向にx座標、画面中央を原点0として左右にy座標とする座標系をとることとする。パソコンの画面(例えば縦25x横80)にグラフを描く場合にスケーリングと呼ばれる座標系の変換を行わなければならない。この場合、縦0から360度横−1から1の実数平面を24x80の整数平面に変換しなければならない。例えば1行を15度、3カラムを0.1として画面上に整数座標を実現すると、下図のようになる。
-
1 2 3 4 5 6 7 1234567890123456789012345678901234567890123456789012345678901234567890123456789 -1.0 -0.5 0 0.5 1.0 0 + . . . . + . . . . + . . . . + . . . . + 15 | | | | | 30 | | | | | 45 | | | | | 60 | | | | | 75 | | | | | 90 | | | | | 105 | | | | | 120 | | | | | 135 | | | | | 150 | | | | | 165 | | | | | 180 | | | | | 195 | | | | | 210 | | | | | 225 | | | | | 240 | | | | | 255 | | | | | 270 | | | | | 285 | | | | | 300 | | | | | 315 | | | | | 330 | | | | | 345 | | | | | 360 | | | | | -
この座標の場合、sin(0度)=0は0度の行に左から40カラム目に'*'をプロットしなければならない。またsin(90度)=1は、90度の行に左から70カラム目'*'をプロットしなければならない。つまりy=0を40カラム目としてそこから+30カラム目をy=1、−30カラム目をy=−1となるように座標変換をしなければならない。このように座標変換の操作をスケーリングと呼ぶ。
以上まででプログラムの実行結果の出力形式が決定された。ではこの例に対してはどのようなデータ構造が考えられるであろうか。ここで扱う関数sinの描くグラフから考えると、1行づつ関数の値を求め対応する位置に'*'をプロットする方法が簡単に考えられる。次のような手順で行なえばよいであろう。
1.x=0度から360度まで15度きざみに以下(2−4)を繰り返す。
2.point <- scale(sin(x度))
3.xの値出力
4.point の位置に'*'を出力 関数scaleについて
-
y=1の大きさが画面上30カラムであり、左から40カラム目がy=0となっている。よって
point = (int)(sin(x度)*30+40);
とすればよい。sin(x)のとる値は−1から1であり、上式によりpointのとる値は10から70の値であることから、目的の座標系に変換できたことになる。この考え方を採用した場合には、1次元のバッファつまり1行分の情報をためておいてから出力をするための領域
char space[61];
を必要とする。ここでのデータ構造は1次元の座標系であり、実現方法は1次元の文字配列である。以上を考慮するとプログラム5−13ができる。
プログラム5−13
/* 1 */ /* Program 5-13 */ /* 2 */ /* Graph of Sine */ /* 3 */ #include <stdio.h> /* 4 */ #include <math.h> /* 5 */ /* 6 */ #define MAX 70 /* 7 */ #define YEN 360 /* 8 */ /* 9 */ int scale(int x); /* 10 */ /* 11 */ main() /* 12 */ { /* 13 */ char oneline[MAX + 1]; /* 14 */ int x, y, i; /* 15 */ /* 16 */ x = 0; /* 17 */ oneline[MAX] = '\0'; /* 18 */ for(i = 1; i < MAX; i++) /* 19 */ printf("%d", i % 10); /* 20 */ printf("\n"); /* 21 */ while(x < YEN) /* 22 */ { /* 23 */ for (i = 0; i < MAX; i++) /* 24 */ oneline[i] = ' '; /* 25 */ y = scale(x); /* 26 */ oneline[y] = '*'; /* 27 */ printf("%6d :%s\n", x, oneline); /* 28 */ x += 15; /* 29 */ } /* 30 */ } /* 31 */ /* 32 */ int scale(int x) /* 33 */ { /* 34 */ double rad, pai = 3.14159; /* 35 */ /* 36 */ rad = pai / 180; /* 37 */ return (int)(sin((float)x * rad) * 30.0 + 30.0); /* 38 */ } /* 39 */実行結果
123456789012345678901234567890123456789012345678901234567890123456789 0 : * 15 : * 30 : * 45 : * 60 : * 75 : * 90 : * 105 : * 120 : * 135 : * 150 : * 165 : * 180 : * 195 : * 210 : * 225 : * 240 : * 255 : * 270 :* 285 : * 300 : * 315 : * 330 : * 345 : ****解説***
-
プログラム5−13では、x−y軸が通常と逆転している。それは、1行づつ計算しその都度出力をする処理を行なうために都合がよいこともあった。さらに円のように1つのグラフで同一x座標に2カ所プロットを必要とすることがある。このような場合は、2次元の整数平面を考え
char space[61][21];
のように実現し、全プロットの位置に'*'を確定してから、一度に出力することが考えられる。またx−y軸の逆転も必要としない。 例5−14
-
下記の関数を用い、正葉形を画面に描け。
r=sin(nθ) (ここでは、n=2の時のみ考える)
x=r・sin(θ)
y=r・cos(θ)
考え方
- まず座標を定める。画面上の13行40カラム目を原点(0,0)と定め、x軸を左右にとり3カラム0.1、y軸を上下にとり1行を0.1の大きさとする。このように考えると、2次元の整数平面を実現しなければならない。よって
char [21][61];
のように2次元の文字配列により整数平面を実現する。次のような座標系になる。10 40 70 カラム y -1.0 -0.5 0.0 0.5 1.0 x -1 + . . . . + . . . . + . . . . + . . . . + -0.9 | | | -0.8 | | | -0.7 | | | -0.6 | | | -0.5 | | | -0.4 | | | -0.3 | | | -0.2 | | | -0.1 | | | 0.0 +--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+ 0.1 | | | 0.2 | | | 0.3 | | | 0.4 | | | 0.5 | | | 0.6 | | | 0.7 | | | 0.8 | | | 0.9 | | | 1.0 + . . . . + . . . . + . . . . + . . . . + - 次のような手順で行なう。
-
1.t=0度から360度についてステップ2を繰り返す。
2. rad <- t * 3.1415926565/180 { 度をラジアンにする }
r <- sin(n*rad)
3.space[i][j], i=0,60, j=0,20 を出力
x <- scale( r * cos(rad) )
y <- scale( r * sin(rad) )
space[x][y] <- '*'
プログラム5−14
-
/* 1 */ /* Program 5-14 */ /* 2 */ /* */ /* 3 */ #include <stdio.h> /* 4 */ #include <math.h> /* 5 */ /* 6 */ #define XMAX 60 /* 7 */ #define YMAX 24 /* 8 */ #define YEN 360 /* 9 */ #define N 2 /* 10 */ /* 11 */ int scalex(double x); /* 12 */ int scaley(double x); /* 13 */ /* 14 */ main() /* 15 */ { /* 16 */ char space[XMAX + 1][YMAX + 1]; /* 17 */ int x, y, i, j, t; /* 18 */ double r, rad, pai = 3.14159; /* 19 */ /* 20 */ for (i = 0; i < YMAX; i++) /* 21 */ { /* 22 */ for (j = 0; j < XMAX; j++) /* 23 */ space[j][i] = ' '; /* 24 */ space[XMAX][i] = '\0'; /* 25 */ } /* 26 */ /* 27 */ for (t = 0; t < YEN; t++) /* 28 */ { /* 29 */ rad = (double)t * pai / 180.0; /* 30 */ r = sin(N * rad); /* 31 */ x = scalex(r * cos(rad)); /* 32 */ y = scaley(r * sin(rad)); /* 33 */ space[x][y] = '*'; /* 34 */ } /* 35 */ /* 36 */ printf("\n"); /* 37 */ for (i = 0; i < YMAX; i++) /* 38 */ { /* 39 */ for (j = 0; j < XMAX; j++) /* 40 */ printf("%c", space[j][i]); /* 41 */ printf("\n"); /* 42 */ } /* 43 */ } /* 44 */ /* 45 */ int scalex(double x) /* 46 */ { /* 47 */ return (int)(x * 30.0 + 30.0); /* 48 */ } /* 49 */ /* 50 */ int scaley(double x) /* 51 */ { /* 52 */ return (int)(x * 12.0 + 12.0); /* 53 */ } 実行結果
-
******* ****** *** **** **** *** * *** *** * * *** *** * * ** ** * ** ** ** ** ** * * ** *** ** *** ****** ** ****** ************************ ************************ ****** ** ****** *** ** *** ** * * ** ** ** ** ** * ** ** * * *** *** * * *** *** * *** **** **** *** ****** ******* ***解説***
-
例5−13,5−14では、実現方法のバリエーションが少ないためデータ構造からすぐにデータ型が決ってしまう。次の例では、少し複雑になっている。
演習問題
- 例5−13を2次元整数平面を構成し、作成せよ。
演習問題
- 画面上にきれいな円を描け。画面の縦と横の比率が違うので見かけ上きれいな円を描くためにはスケーリングによる調整が必要である。
例5−15
-
例5−9の例では、1クラス50名分のデータを取り扱ってきた。今回は、さらに10クラスについて同様なことを考えてみよう。例5−1では下の表のように1クラス分のデータを扱える表を考えていた。
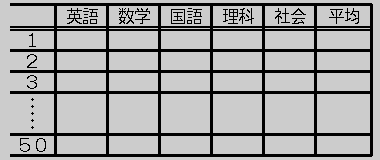
データ構造は上記表である。
実現を考えると各科目の得点は整数値であり、平均値は実数値である。よって
int data[50][5];
のように2つのデータ型を用いていた。
float heikin[50];
さらに、これが10クラス分あるとすると、上記表が10個必要になる。よって、
int data[10][50][5];
のように実現できる。dataは、3次元の整数型の配列、heikinは2次元の浮動小数型の配列である。data[i][j][k]は、iクラスのj番目の生徒のk番目の科目の得点を意味する。さらに、3学年全部を1つの配列でも表現できる。
float heikin[10][50];int data[3][10][50][5];
この場合、data[i][j][k][l]は4次元の整数型配列であり、i学年jクラスのk番目の生徒のl番目の科目の得点を意味する。このように、配列の次元を4次元、さらには5,6,7,...と最大 ○○ 次元まで宣言し、利用することができる。しかし、実際の問題を扱う時にそれほど大きな次元の配列を利用する必要性はごくまれで、2次元せいぜい3次元程度が一般的である。それ以上については、逆にプログラム開発者にとってかえってわかりずらくなることになり、データ構造の設計そのものに問題があると思われる。上記のように4次元配列で実現すると、各添字が何を意味し、また科目が数字に対応していて、プログラミング時に混乱を招くことになるであろう。配列を利用する利点は、4.4節で述べたように添字と繰り返し文を使って同じような処理を簡単にプログラミングできることであるが、より人間の思考に近い形で実現すべきであろう。
float heikin[3][10][50];プログラム5−15
-
/* 1 */ /* Program 5-15 */ /* 2 */ /* 3gakunen 10Class 50nin no seiseki */ /* 3 */ /* 4 */ #include <stdio.h> /* 5 */ /* 6 */ main() /* 7 */ { /* 8 */ int data[3][10][50][5], i, j, k, l; /* 9 */ float heikin[3][10][50], total; /* 10 */ /* 11 */ for (i = 0; i < 3; i++) /* 12 */ for (j = 0; j < 10; j++) /* 13 */ for (k = 0; k < 50; k++) /* 14 */ for (l = 0; l < 5; l++) /* 15 */ scanf("%d", &data[i][j][k][l]); /* 16 */ /* 17 */ for (i = 0; i < 3; i++) /* 18 */ for (j = 0; j < 10; j++) /* 19 */ for (k = 0; k < 50; k++) /* 20 */ { /* 21 */ total = 0.0; /* 22 */ for (l = 0; l < 5; l++) /* 23 */ total += (float)data[i][j][k][l]; /* 24 */ heikin[i][j][k] = total / 5.0; /* 25 */ } /* 26 */ /* 27 */ for (i = 0; i < 3; i++) /* 28 */ for (j = 0; j < 10; j++) /* 29 */ { /* 30 */ for (k = 0; k < 50; k++) /* 31 */ printf(" %10.5f", heikin[i][j][k]); /* 32 */ printf("\n"); /* 33 */ } /* 34 */ } /* 35 */ ***解説***
- ‥‥ない
- 三角関数sinのグラフをキャラクタを用いて描く。
5.3.2 構造体
-
プログラム5−15では、3次元の配列を用いてシンプルなプログラムが書けた。しかし欠点をあげると、前にも述べたように各添字が何を意味し、まして第3の添字が何の科目(英語,数学,国語,理科,社会)に対応しているのかが、暗号のようになっている。当然プログラムを書いた人や内容を少し吟味した人であれば簡単に対応づけができるであろうが、配列の次元や添字が大きくなった時には難しいことであろう。
注意
- 構造体の宣言で用いられる名前の中でプログラムの実行文で実際に使える名前は、構造体の変数名とメンバー名であり、構造体タグ名はプログラムの実行文中には出現しない。それは、タグ名はint,charと同じように型名であり、変数とは扱いが違うからである。
例5−16 整数座標上の2点間の距離(長さ)を求める関数を作る。
考え方
- 2点をa=(ax,bx), b=(bx,by)とすると2点間の距離は、 squareroot( (ax-bx)^2 + (bx-by)^2 ), squarerootは平方根を意味する
で求めることができる。
プログラム5−16
/* 1 */ /* Program 5-16 */ /* 2 */ /* Distance of Points */ /* 3 */ #include <stdio.h> /* 4 */ #include <math.h> /* 5 */ /* 6 */ typedef struct p{ /* 7 */ float x; /* 8 */ float y; /* 9 */ } point_type; /* 10 */ /* 11 */ float distance(point_type a, point_type b); /* 12 */ /* 13 */ main() /* 14 */ { /* 15 */ point_type a, b; /* 16 */ float dis; /* 17 */ /* 18 */ scanf("%f", &a.x); /* 19 */ scanf("%f", &a.y); /* 20 */ scanf("%f", &b.x); /* 21 */ scanf("%f", &b.y); /* 22 */ /* 23 */ dis = distance(a, b); /* 24 */ /* 25 */ printf("%f\n", dis); /* 26 */ } /* 27 */ /* 28 */ float distance(point_type a, point_type b) /* 29 */ { /* 30 */ float dx, dy, dist; /* 31 */ /* 32 */ dx = a.x - b.x; /* 33 */ dy = a.y - b.y; /* 34 */ dist = sqrt(dx * dx + dy * dy); /* 35 */ return dist; /* 36 */ }実行結果
1 2 3 4 2.828427
例5−17
プログラム5−17
/* 1 */ /* Program 5-17 */ /* 2 */ /* */ /* 3 */ #include <stdio.h> /* 4 */ #include <math.h> /* 5 */ /* 6 */ main() /* 7 */ { /* 8 */ struct kojin_type{ /* 9 */ char name[20]; /* 10 */ int eng; /* 11 */ int math; /* 12 */ int japa; /* 13 */ int sci; /* 14 */ int soc; /* 15 */ float heikin; /* 16 */ } data[10][50]; /* 17 */ /* 18 */ int i, j; /* 19 */ float total; /* 20 */ /* 21 */ for (i = 0; i < 10; i++) /* 22 */ for (j = 0; j < 50; j++) /* 23 */ { /* 24 */ total = 0.0; /* 25 */ scanf("%s", &data[i][j].name); /* 26 */ scanf("%d", &data[i][j].eng); /* 27 */ scanf("%d", &data[i][j].math); /* 28 */ scanf("%d", &data[i][j].japa); /* 29 */ scanf("%d", &data[i][j].sci); /* 30 */ scanf("%d", &data[i][j].soc); /* 31 */ total = data[i][j].eng + data[i][j].math + data[i][j].japa + data[i][j].sci + data[i][j].soc; /* 32 */ data[i][j].heikin = total / 5.0; /* 33 */ } /* 34 */ /* 35 */ for (i = 0; i < 10; i++) /* 36 */ for (j = 0; j < 50; j++) /* 37 */ printf("%s : %f\n", data[i][j].name, data[i][j].heikin); /* 38 */ } /* 39 */ /* 40 */実行結果
1 2 3 4 5 6 7 8 triangle ( 1, 2), ( 3, 4), ( 5, 6) move to ( 7, 8) triangle ( 8, 10), ( 10, 12), ( 12, 14)
***解析***
-
構造体は操作しやすいように1つの名前でグループ化された、異なった型の変数の集まりであることがおわかりいただけたであろうか?
さらに、構造体メンバーの宣言に構造体を使うことができる。例えば、三角形は3点で確定される。そこで、三角形という新しい型 triangle_type を宣言してみよう。
struct point_type{ int x_coordinate; int y_coordinate; }; struct triangel_type{ struct point_type p1; struct point_type p2; struct point_type p3; }; struct triangle_type a={ {10,13}, {5,2}, {3,7} };のように宣言できる。triangel_type を構成しているメンバーp1,p2,p3はすでに宣言された構造体 point_type である。この場合、三角形aを構成する1点のx座標は、a.p1.x_coordinate
のように”.”を2回使って参照される。また、変数aの宣言と同時に初期化も行えて3点の座標は、(10,13), (5,2), (3,7) である。10個の三角形を扱う時は、struct triangle_type t[10];
と宣言し、t[5].p2.y_coordinate
のように6つ目の三角形の第2点のy座標を参照できる。もし、int t[10][3][2];
と宣言し、t[5][1][1]
のようにして6つ目の三角形の第2点のy座標を参照するのでは、構造体による宣言とどちらがわかりやすいであろうか。
1つの解決法としてC言語では、構造体と呼ばれる機能を用いることができる。構造体はいくつかのデータ型をまとめてグループ化し、新しいデータ型とするものである。
例えば、座標(x,y)のように2つの数値が組になって1つの値を表わすことがある。このような時は次のように構造体を用いるのが便利であり、分かりやすい。
その1 struct point_type{
int x_coordinate;
int y_coordinate;
};
struct point_type a, b;
その2 struct point_type{
int x_coordinate;
int y_coordinate;
} a, b;
構造体の宣言の一般の形式は、
struct 構造体タグ名{
構造体メンバー;
:
:
};
struct 構造体タグ名 変数名;
または、
struct 構造体タグ名{
構造体メンバー;
:
:
} 変数名;
である。構造体タグ名は、いくつかの型を集めて新しく構成した型名であり、int, char, float と同等(同じような使い方)である。構造体メンバーは、構造体を構成する要素であり、すでに定義されている型もしくはint,charのようにC言語があらかじめ持っている型により定義される。上記座標の例では、point_type が構造体タグ名であり新しい型名とみなすことができる。x_coordinate, y_coordinate は、構造体point_type を構成するメンバー名であり、グループ化された変数名であると考えられる。また、a,bはpoint_type型の変数名である。プログラムでの構造体メンバーの参照は、”.”を使い、
構造体の変数名.メンバー名によって行なわれる。例えば、a.x_coordinate は点aのx座標を意味する。上記例でその1の宣言を1つにまとめたものがその2であるが、ponit_type型の変数を別の場所で宣言することが必要である場合は、その1の方法でないとならない。
-
例5−15を3次元配列ではなく構造体を用いて実現することも可能である。
個人データに関する部分を1つのデータ型として定義すると次のようになる。
struct kojin_type{
char name[20];
int eng;
int math;
int lang;
int sci;
int soc;
float heikin;
};
struct kojin_type data[10][50];
個人に関するデータをkojin_typeという新しいデータ型で宣言したものである。氏名、5科目の点数、5科目の平均点をメンバー名とする。
5.3.3 構造体と関数
-
構造体は新しく定義された型でありchat, int, float と同等であると解説したが、同等であるためには関数の型にも使えなければならない。そこで、本節では構造体で定義された型の関数について解説する。
例5−18 三角形を座標上平行移動させる関数move_triangleを作る。
考え方:
- 引数として三角形(3点の座標)と移動ベクトル(x,y)と与え、戻り値として移動された三角形の座標である。
プログラム5−18
/* 1 */ #include <stdio.h> /* 2 */ /* 3 */ typedef struct s1{ /* 4 */ int x; /* 5 */ int y; /* 6 */ } point_type; /* 7 */ /* 8 */ typedef struct s2{ /* 9 */ point_type p1; /* 10 */ point_type p2; /* 11 */ point_type p3; /* 12 */ } triangle_type; /* 13 */ /* 14 */ triangle_type move_triangle(triangle_type t, point_type p); /* 15 */ /* 16 */ main() /* 17 */ { /* 18 */ triangle_type base_triangle, new_triangle; /* 19 */ point_type vect; /* 20 */ /* 21 */ scanf("%d", &base_triangle.p1.x); /* 22 */ scanf("%d", &base_triangle.p1.y); /* 23 */ scanf("%d", &base_triangle.p2.x); /* 24 */ scanf("%d", &base_triangle.p2.y); /* 25 */ scanf("%d", &base_triangle.p3.x); /* 26 */ scanf("%d", &base_triangle.p3.y); /* 27 */ /* 28 */ scanf("%d", &vect.x); /* 29 */ scanf("%d", &vect.y); /* 30 */ /* 31 */ new_triangle = move_triangle(base_triangle, vect); /* 32 */ /* 33 */ printf("triangle (%3d, %3d), (%3d, %3d), (%3d, %3d)\n" , base_triangle.p1.x, base_triangle.p1.y, base_triangle.p2.x , base_triangle.p2.y, base_triangle.p3.x, base_triangle.p3.y); /* 34 */ printf("move to (%3d, %3d)\n", vect.x, vect.y); /* 35 */ printf("triangle (%3d, %3d), (%3d, %3d), (%3d, %3d)\n" , new_triangle.p1.x, new_triangle.p1.y, new_triangle.p2.x , new_triangle.p2.y, new_triangle.p3.x, new_triangle.p3.y); /* 36 */ } /* 37 */ /* 38 */ triangle_type move_triangle(triangle_type t, point_type p) /* 39 */ { /* 40 */ triangle_type dum; /* 41 */ /* 42 */ dum.p1.x = t.p1.x + p.x; /* 43 */ dum.p2.x = t.p2.x + p.x; /* 44 */ dum.p3.x = t.p3.x + p.x; /* 45 */ dum.p1.y = t.p1.y + p.y; /* 46 */ dum.p2.y = t.p2.y + p.y; /* 47 */ dum.p3.y = t.p3.y + p.y; /* 48 */ return dum; /* 49 */ } /* 50 */***解説***
解説がない例5−19 モンテカルロ法により円周率πを推定し、同時に画面上に4分の1円を描け。
考え方:
-
モンタカルロ法は、1945年ごろ数学者J.v.ノイマンとS.M.ユラムによって決定論的な数学の問題を乱数を使って解くために考案された方法である。最近では、シミュレーションに利用される。
今、原点(0,0)と(1,1)で特定された1x1の正方形と原点と中心とし半径1の4分の1円(扇型)が同じ座標上に存在するとする。この時、0から1の乱数により適当な座標をN個発生(正方形内のある点)させ、その中で4分の1円内に入る座標をM個とする。円周率をπとすると、正方形の面積は1(1*1)であり、扇の面積はπ/4(1*1*π/4)である。乱数により多くの座標上の点を発生させると、
正方形の面積 : 扇の面積 = N : M
という関係に近づく。よって、1 : π/4 = N : M
から、π = 4*M/N
という関係式が導きだせ、πが推定できる。このように、円周率π=3.14159265... と既知なものを乱数を用いて、もとめる手法をモンテカルロ法という。
手順
-
pointのプロットについては、スケーリングを行い画面いっぱいに正方形と扇が描けるようにする。- 0〜1の乱数を発生させる関数randを作る。
- N,M <− 0に初期化する。 MAX <− 発生させる座標の数を与える。
- 乱数の初期値aを適当に与える。
- 2つの乱数を発生させ、座標をつくる。 ( x <− rand(a); y <− rand(a); point <− (x,y); )
- N <− N+1
- もし、 pointが扇の内部であれば M <− M+1; pointをプロットする;
- もし、N<MAX であれば ステップ4へ
- 円周率の出力( 4*M/N ), 扇の出力
- おわり
プログラム5−19
/* 1 */ /* Program 5-19 */ /* 2 */ /* Calculate PAI by Montecarlo Method */ /* 3 */ #include <stdio.h> /* 4 */ #include <stdlib.h> /* 5 */ #include <math.h> /* 6 */ #include <time.h> /* 7 */ /* 8 */ #define MAX 10000 /* 9 */ #define TANE 44 /* 乱数の種 お好きな数をどうぞ */ /* 10 */ /* 11 */ typedef struct t{ /* 12 */ double x; /* 13 */ double y; /* 14 */ } point_type; /* 15 */ /* 16 */ unsigned double rnd(double a); /* 17 */ /* 18 */ main() /* 19 */ { /* 20 */ int n, m, i, j, x, y; /* 21 */ double pai, d; /* 22 */ char space[40][20]; /* 23 */ point_type apoint; /* 24 */ /* 25 */ m = 0; /* 26 */ n = 0; /* 27 */ for (i = 0; i < 40; i++) /* 28 */ for (j = 0; j < 20; j++) /* 29 */ space[i][j] = ' '; /* 30 */ apoint.x = rnd((double)TANE); /* 31 */ apoint.y = rnd(apoint.x); /* 32 */ /* 33 */ while(n < MAX) /* 34 */ { /* 35 */ n++; /* 36 */ apoint.x = rnd(apoint.x); /* 37 */ apoint.y = rnd(apoint.y); /* 38 */ d = sqrt(apoint.x * apoint.x + apoint.y * apoint.y); /* 39 */ if (d < 1.0) /* 40 */ { /* 41 */ x = (int)(apoint.x * 40); /* 42 */ y = 19 - (int)(apoint.y * 20); /* 43 */ space[x][y] = '*'; /* 44 */ m++; /* 45 */ } /* 46 */ } /* 47 */ pai = 4.0 * (double)m / (double)n; /* 48 */ printf(" PAI = %f\n", pai); /* 49 */ for (i = 0; i < 20; i++) /* 50 */ { /* 51 */ for (j = 0; j < 40; j++) /* 52 */ printf("%c", space[j][i]); /* 53 */ printf("\n"); /* 54 */ } /* 55 */ /* 56 */ } /* 57 */ /* 58 */ unsigned double rnd(double a) /* 59 */ { /* 60 */ double dum; /* 61 */ long mod; /* 62 */ /* 63 */ mod = ((23 * (int)(a * time(&mod))) % 32749) % 10000; /* 64 */ dum = (double)mod / 10000; /* 65 */ if(dum < 0) /* 66 */ dum = -dum; /* 67 */ return dum; /* 68 */ }実行結果
PAI = 3.183600 ************ ***************** ******************** ************************ ************************** ***************************** ******************************* ******************************** ********************************** *********************************** ************************************ ************************************* ************************************* ************************************** *************************************** **************************************** **************************************** **************************************** **************************************** ****************************************
***解説***
- かいせつがない
CONTENTS / BACK-PAGE / NEXT-PAGE