今回からは、アルゴリズムを中心に解説を行なっていきたいと思います。

６．並べ換えの問題

　大容量のデータを扱う際に、データをある規則に準じて整列し格納されていることが多い。我々が通常目にする多くの種類のデータは、たいていそのようになっている。例えば、学生に関するデータは学籍番号順（五十音順）に並んで保管されている。図書館に行ってみても、蔵書目録カードは、書籍名の五十音順と著者名の五十音順に並べられている。さらに、病院のカルテの保管も生年月日順であったり、五十音順であったりする。このように、データをなんらかの目的に応じて、整列させていることがほとんどである。それは、データの検索や参照を考えると、より早い時間で目的のデータが得られ易いからである。

　このように、並べ換えの問題は我々にとって身近な問題である。本節では、代表的な並べ換えの方法を紹介するとともに、プログラムの効率（アルゴリズムの速さ）について議論する。並べ換えを英語ではソート（sort）と呼ぶ。そのため、並べ換えのアルゴリズムをソーティングアルゴリズムと言う。

---

６．１　ソーティングアルゴリズムの種類と計算の手間

　トランプ（ハートマークのみ１３枚）を１から順に整列させることを考えてみよう。ある人は、１３枚手に持ちまず１を見つけそれを一番左に移動させ、次に２を見つけ左から２番目に移動させ、・・・を繰り返し、最後には１から順に並べることをするでしょう。ある人は、手にとったカードで隣会ったカードを比べ、大きい方を右へずらし、順次全てのカードに対して行なうことにより、並び換えるでしょう。またある人は、１３枚床にばらまき１から順に拾って並べることをするでしょう。このように、カードの並べ換えの方法はいろいろ考えられるように、コンピュータを使ったデータの並べ換えにも多くの手法（アルゴリズム）が提案されている。代表的なものをまとめると、表６−１のようになる。

表６−１ ソーティングアルゴリズムの種類

分類	低速アルゴリズム	高速アルゴリズム
選択法	単純選択ソート	ヒープソート
挿入法	単純挿入ソート	シェルソート（注意＊１）
交換法	バブルソート シェーカーソート	クイックソート
併合法	−−−	マージソート

　表６−１において低速、高速で分類しているが、アルゴリズムの速さとは実行に要する計算の手間である。理論計算機科学の分野では、この計算の手間を計算量（計算時間量）と呼び、アルゴリズムの計算量について多くの研究が行なわれている。この計算量はアルゴリズムの評価の第一の基準となっている。たとえ、どんなに簡単なアルゴリズムでも目的の結果が得られるまでに、何十年もかかってはまったく意味の無いものとなってしまう。

　ソーティングアルゴリズムについて言うと、低速アルゴリズムはＯ（ｎ＾２）、高速アルゴリズムはＯ（ｎｌｏｇｎ）に分類できる。Ｏ（オーダーもしくはビッグオー）とは、計算量を評価するときの単位で、対象とするデータの数ｎに比例して計算の手間が多くなることを意味する。ソーティングアルゴリズムの場合は、比較演算あるいは交換演算の回数が対象データの数の２乗もしくはｎｌｏｇｎに比例して多くなる。例えば対象データの数を１００倍すると、高速アルゴリズムでは約６６４倍（１００＊ｌｏｇ2（１００））に、低速アルゴリズムでは１００００倍（１００＊１００）になる。

　このように、データの数が多くなったときに与えたアルゴリズムが本当に有効なものなのかを知る手掛かりとして、計算量を評価することは重要なことである。一般にアルゴリズムの計算量を評価する方法として、

　１．データの大きさに対する平均計算時間の増加率が小さいほどよい，
　２．最悪ケースを考えた時のオーダーが小さいほどよい，
　３．計算時間の分散が少ないほどよい，

の順に評価することがよいとされている。

　アルゴリズムの優劣は、計算時間量の他にも、計算時の記憶域の少なさや、ステップ数、エレガントさなどがある。

　本章では、いくつかのソーティングアルゴリズムを紹介するとともに、計算量の評価の仕方について学ぶ。

注意＊１：

シェルソートを高速アルゴリズムに分類したが、計算量はＯ（ｎ＾１．２）であることが知られている。

---

６．２　低速アルゴリズム

　本節では、いくつかの低速アルゴリズムを紹介する。

（１）単純選択ソート

　ソーティングのなかではもっとも簡単な手法が、単純選択ソートである。 説明を簡単にするために、以下のようなデータの列を考えよう。

49　 66　 11　 37　 84　 6　 22　 73

与えられたデートの左から順に見ていき、最小のものを見つける。この場合６が最小データである。その最小データと一番左のデータを入れ換える。

6　 66　 11　 37　 84　 49　 22　 73

次に、左から２番目のデータから右へ順に最小のデータを捜す。１１が最小である。２番目のデータ（６６）と最小のデータ（１１）を入れ換える。

6　 11　 66　 37　 84　 49　 22　 73

同様に左から３番目のデータから順に最小データを捜し、３番目（６６）と最小データ（２２）を入れ換える。

6　 11　 22　 37　 84　 49　 66　 73

以下、同様な操作を繰り返すと、

6　 11　 22　 37　 49　 84　 66　 73

6　 11　 22　 37　 49　 66　 84　 73

6　 11　 22　 37　 49　 66　 73　 84

となり、並べ換えが終了する。

この考えを取り入れたプログラミングが次のプログラム６−１である。

---

/*   1 */  /*  Program 6-1   */
/*   2 */  /*   Simple Selection Sort   */
/*   3 */
/*   4 */  #include<stdio.h>
/*   5 */  #define  MaxNumber  100
/*   6 */  #define INIT  1984
/*   7 */
/*   8 */  void SimpleSelection( int data[], int n );
/*   9 */  void Outputdata( int data[], int n );
/*  10 */  void Makedata( int data[], int n );
/*  11 */  int rnd(void);
/*  12 */
/*  13 */  main()
/*  14 */  {
/*  15 */       int data[MaxNumber], i;
/*  16 */       
/*  17 */       Makedata(data, MaxNumber);
/*  18 */       SimpleSelection(data, MaxNumber);
/*  19 */       Outputdata(data, MaxNumber);
/*  20 */  }
/*  21 */
/*  22 */  void SimpleSelection(int data[], int n)
/*  23 */  {
/*  24 */       int min, tmp, i, j, min_id;
/*  25 */
/*  26 */       for (i=0; i < n-1; i++)
/*  27 */       {
/*  28 */               min = data[i];
/*  29 */               for (j=i+1; j < n; j++)
/*  30 */                       if(data[j] < min)
/*  31 */                       {
/*  32 */                               min = data[j];
/*  33 */                               min_id = j;
/*  34 */                       }
/*  35 */               tmp = data[i];
/*  36 */               data[i] = data[min_id];
/*  37 */               data[min_id] = tmp;
/*  38 */       }
/*  39 */  }
/*  40 */
/*  41 */  void Outputdata(int data[], int n)
/*  42 */  {
/*  43 */       int i;
/*  44 */       
/*  45 */       for (i=0; i < n; i++)
/*  46 */       {
/*  47 */                   printf("%8d", data[i]);
/*  48 */       }
/*  49 */  }
/*  50 */
/*  51 */  void Makedata( int data[], int n)
/*  52 */  {
/*  53 */       int i;
/*  54 */
/*  55 */       for (i=0; i < n; i++)
/*  56 */               data[i] = rnd();
/*  57 */  }
/*  58 */
/*  59 */  int rnd(void)
/*  60 */  {
/*  61 */       static unsigned long mod = INIT;
/*  62 */
/*  63 */       mod = (23 * mod) % 32749;
/*  64 */       return mod;
/*  65 */  }

---

　プログラム６−１を簡単に説明する。まず、乱数を用いて並べ換えを行なうデータを１００個生成する。これが Makedata である。次に、SimpleSelection により、生成したデータを単純選択ソートにより並べ換えをする。最後に、並べ換えを終えたデータをOutputdataにより出力する。

　SimpleSelection においては、２８−３４で最小データを捜し最小値とその配列の添字を求めている。３５−３７で、最小値と対象としている一番左側のデータとの入れ換えを行なっている。

　SimpleSelectionの各ステップの実行回数を評価してみよう。２６−３８を見ると、２６，２９のｆｏｒの２重のループ（繰り返し）になっていることに気付く。２６のｆｏｒループにより、２６，２７，２８，３５，３６，３７はｎ回（今回はｎ＝１００となっている）実行することがわかる。

　２９のｆｏｒループの内側の実行回数を考える。２６でｉ＝０の時、２９ではｊは１からｎ−１までを繰り返すので、この時３０はｎ−１回実行する。続いて、２６でｉ＝１の時、２９ではｊは２からｎ−１まで繰り返すので、この時３０はｎ−２回実行する。以下同様に、ｉ＝ｎ−２まで繰り返すと、３０の実行回数は（ｎ−１）＋（ｎ−２）＋・・・＋１となり、ｎ＊（ｎ−１）／２回となる。

　３２，３３の実行回数は、３０のｉｆの判定に依存する。３０の判定が真になる確率を考えなければならないが、ここではラフに１／２としよう。すると、２３，３３の実行回数は、３０の実行回数の１／２と考えられるため、ｎ＊（ｎ−１）／４回となる。これですべての実行回数が求まった。

　プログラム６−１の計算量は、比較演算回数と入れ換えの回数に着目すると、３０，３２，３３の実行回数を考えればよい。つまり、ｎ＊（ｎ−１）／２とｎ＊（ｎ−１）／４である。今、ｎの値をとてつもなく大きくすることを考えると、−１が無視できｎ＝ｎ−１と考えられる。同様に、１／２も１／４もｎがすごく大きい時には、無視できる。ｎが大きいとき３０，３２，３３は、約ｎ＊ｎ（ｎ＾２）回実行されると考えられる。よって、プログラム６−１の計算量はＯ（ｎ＾２）であることが言える。

---

（２）バブルソート

　バブルソートは単純選択ソートを少し変形したもので、最小値を求めることをせずに、左から順に隣会った左右のデータを比べ、左側のデータが大きい時にはすぐに入れ換えを行なう方法である。バブルとは泡を意味していて、データが下から上へ泡立つ（左から右へ順に大きくなる）ように並べ換えが行なわれることから、泡立ち法とも呼ばれている。下記の例で、その動きを見よう。

　　49   66   11   37   84   6   22   73

まず、４９と６６を比べ４９の方が小さいのでなにもしない。

　　49   66   11   37   84   6   22   73

続いて、６６と１１を比べ１１の方が小さいので１１と６６を入れ換える。

　　49   11   66   37   84   6   22   73

さらに、６６と３７を比べ３７の方が小さいので６６と３７を入れ換える。

　　49   11   37    66   84   6   22   73

以下、一番右のデータまで繰り返す。

　　49   11   37    66   6   22   73   84

すると、一番右側に最大のデータがくる。上記の操作を、左から順に右から２番目までのデータに対して行なう。

    11   37   49    6    22   66   73   84

すると、右から２番目には２番目に大きいデータがくる。このように、上記操作を続けると最後には左から昇順にデータは並ぶことになる。

　　6   11   22   37   49   66   73   84

上記のデータの動きからも、泡立つ様子がうかがえたことでしょう。

---

/*   1 */  /*  Program 6-2   */
/*   2 */  /*   Bublle Sort   */
/*   3 */
/*   4 */  #include<stdio.h>
/*   5 */  #define  MaxNumber  100
/*   6 */  #define INIT  1984
/*   7 */
/*   8 */  void BublleSort( int data[], int n );
/*   9 */  void Outputdata( int data[], int n );
/*  10 */  void Makedata( int data[], int n );
/*  11 */  int rnd(void);
/*  12 */
/*  13 */  main()
/*  14 */  {
/*  15 */       int data[MaxNumber], i;
/*  16 */       
/*  17 */       Makedata(data, MaxNumber);
/*  18 */       BublleSort(data, MaxNumber);
/*  19 */       Outputdata(data, MaxNumber);
/*  20 */  }
/*  21 */
/*  22 */  void BublleSort(int data[], int n)
/*  23 */  {
/*  24 */       int tmp, i, j;
/*  25 */
/*  26 */       for (i=0; i < n-1; i++)
/*  27 */               for (j=0; j < n-i-1; j++)
/*  28 */                       if(data[j] > data[j+1])
/*  29 */                       {
/*  30 */                               tmp = data[j];
/*  31 */                               data[j] = data[j+1];
/*  32 */                               data[j+1] = tmp;
/*  33 */                       }
/*  34 */  }
/*  35 */
/*  36 */  void Outputdata(int data[], int n)
/*  37 */  {
/*  38 */       int i;
/*  39 */       
/*  40 */       for (i=0; i < n; i++)
/*  41 */                   printf("%8d", data[i]);
/*  42 */  }
/*  43 */
/*  44 */  void Makedata( int data[], int n)
/*  45 */  {
/*  46 */       int i;
/*  47 */
/*  48 */       for (i=0; i < n; i++)
/*  49 */               data[i] = rnd();
/*  50 */  }
/*  51 */
/*  52 */  int rnd(void)
/*  53 */  {
/*  54 */       static unsigned long mod = INIT;
/*  55 */
/*  56 */       mod = (23 * mod) % 32749;
/*  57 */       return mod;
/*  58 */  }
/*  59 */

---

　関数 Makedata, Outputdata, rnd はプログラム６−１で使ったものと同じである。ソートのアルゴリズムのみが換わっている。プログラム６−１同様、各実行文の実行回数を評価してみよう。評価結果は以下のようである。

　　　２６行目　　　　ｎ　回
　　　２７　　　（ｎ−１）＊ｎ／２　回
　　　　　　　　　　　　　　　　　（　（ｎ−１）＋（ｎ−２）＋・・・ ＋１　）
　　　２８　　　（ｎ−１）＊ｎ／２　回
　　　３０　　　（ｎ−１）＊ｎ／４　回
　　　３１　　　（ｎ−１）＊ｎ／４　回
　　　３２　　　（ｎ−１）＊ｎ／４　回

よって、バブルソートも単純選択ソートと同様Ｏ（ｎ＾２）の計算量を持つことが示せた。

---

（３）シェーカーソート

　シェーカーソートは、基本原理はバブルソートを用いる。バブルソートの場合、常に左から右へ比較を行い右側に最大値をもってきている。シェーカーソートは、左から右へ比較を行い最大値を固定した後は、逆に右から左へ比較を行い最小値を左側に固定する。この操作を繰り返し行なうことにより、データの並べ換えを実現する。理解を深めるために、下記に例を示そう。

　　49   66   11   37   84   6   22   73

まず、左から右へバブルソートを行い、一番右側に最大値を固定する。

　　49   11   37    66   6   22   73   84
                                       ^
次に、固定した８４を除いて、右から左へ向かってバブルソートを行なう。

    6   49   11   37   66   22   73   84
    ^                                 ^
すると、一番左側に最小データが固定される。つづいて、固定された６と８４を
除いて左から右へ向かってバブルソートを行なう。

    6   11   37   49   22   66   73   84
    ^                            ^    ^
７３が８４を除いた最大値として固定される。さらに、右から左へ向かってバブ
ルソートを行なう。

    6   11   22   37   49   66   73   84
    ^   ^                        ^    ^
１１が６を除いた最小値として固定される。以下、上記操作を繰り返しおこなう。

  6   11   22   37   49   66   73   84
  ^   ^                   ^    ^    ^
  6   11   22   37   49   66   73   84
  ^   ^    ^              ^    ^    ^
  6   11   22   37   49   66   73   84
  ^   ^    ^         ^    ^    ^    ^
  6   11   22   37   49   66   73   84
  ^   ^    ^   ^     ^    ^    ^    ^

上記例では、固定された数値には＾マークを付けて、固定される順番がわかりやすくした。

---

＜演習問題＞

シェーカーソートのプログラムを作成し、計算量の評価をしてみよう。

---

（４）単純挿入ソート

　単純挿入ソートは、対象とするデータがリストのようなときにはとても有効である。しかし、単なる配列データの時には、基本的な考え方はバブルソートと同じである。また、例をあげて解説しよう。

　　49   66   11   37   84   6   22   73

単純挿入法では、あらかじめ並べ換えが済んでいるデータ列に新たにデータを挿入する事を基本としている。そこで、まず左から１番目までが並べ換えが済んでいるとして、２番目のデータをそこに挿入することを考える。この例では、４９が１つしかないデータ列に６６を挿入することを考える。この場合は、なんの変化もない。

　　49   66   11   37   84   6   22   73

次に、４９，６６のデータ列に１１を挿入することを考える。大きい方から小さい方（右から左へ）に向かって比較していき、ソート済みのデータ列のどこに挿入できるかを見ていく。この場合は、１１が一番小さいため一番左に挿入されたことになる。

    11   49   66   37   84   6   22   73

次に、１１，４９，６６のデータ列に３７を挿入する。６６から左へ順に見ていく。

    11   37   49   66   84   6   22   73

以下、同様な操作を行なう。

    11   37   49   66   84    6   22   73

     6   11   37   49   66   84   22   73

     6   11   22   37   49   66   84   73

     6   11   22   37   49   66   73   84

以下のような、プログラムが作成できる。

---

/*   1 */  /*  Program 6-3   */
/*   2 */  /*   Simple Insertion Sort   */
/*   3 */
/*   4 */  #include<stdio.h>
/*   5 */  #define  MaxNumber  100
/*   6 */  #define INIT  1984
/*   7 */
/*   8 */  void SimpleInsertion( int data[], int n );
/*   9 */  void Outputdata( int data[], int n );
/*  10 */  void Makedata( int data[], int n );
/*  11 */  int rnd(void);
/*  12 */
/*  13 */
/*  14 */
/*  15 */  main()
/*  16 */  {
/*  17 */       int data[MaxNumber], i;
/*  18 */       
/*  19 */       Makedata(data, MaxNumber);
/*  20 */       SimpleInsertion(data, MaxNumber);
/*  21 */       Outputdata(data, MaxNumber);
/*  22 */  }
/*  23 */
/*  24 */  void SimpleInsertion(int data[], int n)
/*  25 */  {
/*  26 */       int tmp, i, j;
/*  27 */
/*  28 */       for( j=1; j < n; j++ )
/*  29 */       {
/*  30 */               i = j - 1;
/*  31 */               tmp = data[j];
/*  32 */               while( (i>=0) && (tmp<data[i]) )
/*  33 */               {
/*  34 */                       data[i+1] = data[i];
/*  35 */                       i = i - 1;
/*  36 */               }
/*  37 */               data[i+1] = tmp;
/*  38 */       }
/*  39 */  }
/*  40 */
/*  41 */  void Outputdata(int data[], int n)
/*  42 */  {
/*  43 */       int i;
/*  44 */       
/*  45 */       for (i=0; i < n; i++)
/*  46 */       {
/*  47 */                   printf("%8d", data[i]);
/*  48 */       }
/*  49 */  }
/*  50 */
/*  51 */  void Makedata( int data[], int n)
/*  52 */  {
/*  53 */       int i;
/*  54 */
/*  55 */       for (i=0; i < n; i++)
/*  56 */               data[i] = rnd();
/*  57 */  }
/*  58 */
/*  59 */  int rnd(void)
/*  60 */  {
/*  61 */       static unsigned long mod = INIT;
/*  62 */
/*  63 */       mod = (23 * mod) % 32749;
/*  64 */       return mod;
/*  65 */  }

---

　単純挿入ソートもＯ（ｎ＾２）の計算量を持つことは、２８のｆｏｒループ内に３２のｗｈｉｌｅループが存在することから予想できる。単純選択ソートと同様な方法で容易に示せる。

　以上、４種類の低速アルゴリズムを示した。これらのアルゴリズムは単純であるが、Ｏ（ｎ＾２）の計算量を持つことが理解できたであろう。このｎ＾２のオーダーがどの程度のものなのかは、ｙ＝ｘ＾２のグラフを方眼紙に書いてみるとよい。ｘがある数値を越えると、ｙが急に大きくなり方眼紙をはみ出してしまう。このように、データの個数がある点を越えると、ソートにとてつもなく時間を要するようになるということである。

---

＜上級演習問題＞

　本説で、紹介した４つのアルゴリズムについてデータの個数の限界の目安をつける。

方法：

実行時間を計る内部関数（コンパイラに依存しますが、time, clock など）を用いて、データの個数とソートに要した時間の関係を調べる。その結果をグラフにして、急に時間が大きくなったあたりのデータの数が、限界であると判断する。

　まず、以下のような表を作成するとよい。

	　データの数　│　 実行時間
	━━━━━━━━━━━━━━━
	　　　１００　│
	───────┼───────
	　　　２００　│
	───────┼───────
		：
		：
	───────┼───────
	　　１０００　│
	───────┼───────
	　　３０００　│
	───────┼───────
	　　５０００　│
	───────┼───────
	　１００００　│
	───────┼───────
		：
		：

　このように、適当なデータの数を設定し、ソートに要した時間を計測する。

---

６．３　高速アルゴリズム

　本節では、６．２節で紹介した並べ換えのアルゴリズムよりも高速に処理ができるアルゴリズムを紹介する。ここで高速と呼んでいるものは、Ｏ（ｎ　ｌｏｇ　ｎ）に分類できるものである。

---

（１）　クイックソート

　クイックソートは世の中で最も速いソートアルゴリズムとして知られている。（これは、一つのＣＰＵで順次処理を行なった場合である。最近では、計算機の機能が高まり、並列処理や分散処理が可能となっているため、複数のＣＰＵを持った計算機上での並べ換えについては、クイックソートよりも速いアルゴリズムが提案されている。）

　クイックソートは、データの分割法をソートのアルゴリズムに適用した典型なものである。データ分割法の基本原理は、

        １　データのブロック分割
        ２　各ブロックごとの処理（並べ換え）
        ３　ブロックの統合

であり、クイックソートでは特に１のデータの分割にアルゴリズムのよさの秘密が隠されている。例を用いてクイックソートのアルゴリズムを解説しよう。

例
	　入力データ： 48  65  10  36  83   5  21  72

　ステップ０１　まず与えられたデータ列の真ん中（左から４番目）に位置する データを基準値をして定める。例では、３６と基準値としよう。

	 48  65  10  36  83   5  21  72
	  ^           ^           ^

　ステップ０２　データを左から順に基準値よりも大きいデータを捜す。まず４８が見つかる。続いて、右から順に基準値よりも小さいデータを捜す。 ２１が見つかる。ここで、４８と２１を入れ替えする。現在注目しているデータの位置を次に進める（左から見ている場合は一つ右へ、右からの場合は左へ一つ進める）。

	21  65  10  36  83   5  48  72
	     ^       ^       ^

さらに、ステップ０２を続けると、５と６５が入れ替わる。

	21   5  10  36  83  65  48  72
	     ^       ^       ^

以下、同様な操作を繰り返し、注目している点が交差するまで行なう。すると

	21   5  10  36  83  65  48  72

が得られる。これは、基準値とした位置（左から４番目）を境に、左右ブロックに分割したことになる。左側には４番目のデータ（３６）よりも小さいデータ、右側には大きいデータとなる。

　ステップ１−１　左側のブロックに対して、ステップ０１，０２を行なう。

	21   5  10
	     ^
	 5  21  10

　 　よって、５と２１，１０とに分割できる。

　ステップ１−１−１　さらに、左側についてステップ０１，０２を行なう。この場合、５だけなのでなにもしない。

　ステップ１−１−２　右側の２１，１０についてステップ０１，０２を行なう。

上記ステップ１−１−１，１−１−２により、 5 10 21 が得られる。

　ステップ１−２　８３，６５，４８，７２について同様にステップ０１，０２を行なう。 よって、 5 10 21 36 48 65 72 83　が得られる。

　基準点としたデータが、左、右いずれかのブロックに含まれる時と含まれない時がある。その詳細についてはプログラム６−４を見ていただきたい。ここでは、アルゴリズムの大体の考え方を理解できればよいと考えている。

　クイックソートのプログラムは以下のようである。

---

/*   1 */  /*  Program 6-4   */
/*   2 */  /*   Quick Sort   */
/*   3 */
/*   4 */  #include<stdio.h>
/*   5 */  #define  MaxNumber  100
/*   6 */  #define INIT  1984
/*   7 */
/*   8 */  void QuickSort( int data[], int lowert, int upper );
/*   9 */  void Outputdata( int data[], int n );
/*  10 */  void Makedata( int data[], int n );
/*  11 */  int rnd(void);
/*  12 */
/*  13 */
/*  14 */
/*  15 */  main()
/*  16 */  {
/*  17 */       int data[MaxNumber], i;
/*  18 */       
/*  19 */       Makedata(data, MaxNumber);
/*  20 */       QuickSort(data, 0, MaxNumber-1);
/*  21 */       Outputdata(data, MaxNumber);
/*  22 */  }
/*  23 */
/*  24 */  void QuickSort( int data[], int upper, int lower )
/*  25 */  {
/*  26 */       int mid, tmp, i, j;
/*  27 */
/*  28 */       i = upper;
/*  29 */       j = lower;
/*  30 */       mid = data[(lower+upper)/2];
/*  31 */       do
/*  32 */       {
/*  33 */               while( data[i] < mid ) i++;
/*  34 */               while( mid < data[j] ) j--;
/*  35 */               if( i <= j )
/*  36 */               {
/*  37 */                       tmp = data[i];
/*  38 */                       data[i] = data[j];
/*  39 */                       data[j] = tmp;
/*  40 */                       i++;
/*  41 */                       j--;
/*  42 */               }
/*  43 */       } while( i <= j );
/*  44 */       if ( upper < j ) QuickSort(data, upper, j);
/*  45 */       if ( i < lower ) QuickSort(data, i, lower);
/*  46 */  }
/*  47 */
/*  48 */  void Outputdata(int data[], int n)
/*  49 */  {
/*  50 */       int i;
/*  51 */       
/*  52 */       for (i=0; i < n; i++)
/*  53 */       {
/*  54 */                   printf("%8d", data[i]);
/*  55 */       }
/*  56 */  }
/*  57 */
/*  58 */  void Makedata( int data[], int n)
/*  59 */  {
/*  60 */       int i;
/*  61 */
/*  62 */       for (i=0; i < n; i++)
/*  63 */               data[i] = rnd();
/*  64 */  }
/*  65 */
/*  66 */  int rnd(void)
/*  67 */  {
/*  68 */       static unsigned long mod = INIT;
/*  69 */
/*  70 */       mod = (23 * mod) % 32749;
/*  71 */       return mod;
/*  72 */  }

---

　関数Quicksortは、プログラム内部でさらに自分自身を関数として呼んでいる。つまり再帰的なアルゴリズムとなっている。先に示した例のデータを用いて実行の様子を表現すると、下記のような構造となっている。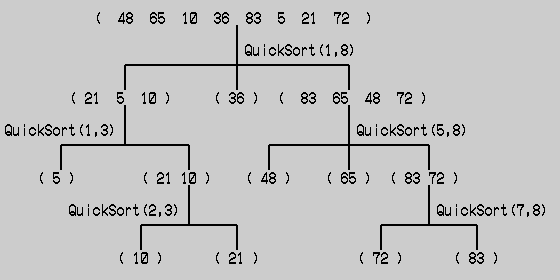

よって分割したブロックを統合すると、

        5  10  21  36  48  65  72  83

となる。

　クイックソートの計算時間量を評価してみよう。今回は、プログラム中の３７−３９の実行回数をカウントすることで、オーダーを求めることにする。

１段目	QuickSort(1,n)では、入れ替えの起こる確率を１／２とすると約ｎ／２回実行される。
２段目	QuickSort(1,n/2)、QuickSort(n/2,n)では、入れ替えの起こる確率を１／２とするとそれぞれ約ｎ／４回実行される。二つの回数を合わせると、約ｎ／２回の実行となる。
３段目	４つの関数QuickSort(1,n/4)、QuickSort(n/4,n/2)、QuickSort(n/2,3n/4)、QuickSort(3n/4,n)が実行されそれぞれ約ｎ／８回の実行となる。これらを合わせると約ｎ／２回の実行となる。
４段目	同様に考えると８回のQuickSort関数を実行し、それぞれ約ｎ／１６回実行。合わせると約ｎ／２回の実行回数となる。

　以上から、各段階では約ｎ／２回の入れ替えが起こることがわかる。

　上記分割が何回（何段まで）起こるかを考えよう。１回の関数の実行では２つに分割され、それらがさらに２つに分割される。これが１つのデータとなるまで繰り返される。よって分割の回数は、ｌｏｇ（ｎ）回であると言える。ここで、ｌｏｇとは数学の対数関数を意味し、この場合の対数の底は２である。　ｎ＝２＾ｋ（ｎが２のｋ乗）である時、ｋ＝ｌｏｇ（ｎ）である。

　よって、プログラム３７−３９の実行回数は、ｎ／２　＊　ｌｏｇ（ｎ）　回となり、プログラム４−６はＯ（ｎｌｏｇｎ）であると言える。これは、前節で示したＯ（ｎ＾２）のアルゴリズムと比較すると、非常に効率がよいことがわかる。

　今回の解説では分割の基準点を中心として行なったが、先頭データを基準点とする方法もある。完全にランダムなデータに対しては、基準点をどちらに設定しても同じ計算の手間で実行される。しかし、すでに並べ替えが完了しているデータに対して、先頭のデータを基準点とする方法を適用すると、最悪ケースとなりＯ（ｎ＾２）の計算量となることが知られている。

---

演習問題

ｙ＝ｘ＾２　と　ｙ＝ｘ＊ｌｏｇ（ｘ）　の関数のグラフを書いてみよう（対数の底を２と考える）。グラフの増加の様子から、ｘがどのくらいになるとｙがとてつもなく大きくなるかを調べよ。

---

（２）ヒープソート

　ヒープ（heap）とは、以下の条件を満たす２分木のことである。２分木とは、１つの頂点から２本以下の枝が出ている木のことであり、計算機分野では重要な構造の１つである。２分木の構成方法や応用については第７節を予定している。

　ヒープ：２分木の各頂点には次の２式を満たさなければならない。
            １．　ｈ(i) ≧ ｈ(2i)     i=1,2,3,...
            ２．　ｈ(i) ≧ ｈ(2i+1)   i=1,2,3,...

　つまり、２分木の各頂点に位置するデータの値は、常に上に位置するデータの値以下になっていなければならない。

例
　　　　　　　　　　　　　　　　 ｈ(1)
　　　　　　　　　　　　　　　　　│
　　　　　　　　　┌───────┴───────┐
　　　　　　　　 ｈ(2)　　　　　　　　　　　　　 ｈ(3)
　　　　┌────┴────┐　　　　　　┌───┴───┐
　　　 ｈ(4)　　　　　　　 ｈ(5)　　　　 ｈ(6)　　　　　 ｈ(7)
　┌──┴──┐　　　┌──┴──┐
 ｈ(8)       ｈ(9)   ｈ(10)

　この場合、ｈ(1)≧ｈ(2),ｈ(3)
　　　　　　ｈ(2)≧ｈ(4),ｈ(5)
　　　　　　ｈ(3)≧ｈ(6),ｈ(7)
　　　　　　ｈ(4)≧ｈ(8),ｈ(9)
　　　　　　ｈ(5)≧ｈ(10)

である。ヒープによる並べ換えは、ヒープがすでに与えられているものとして、ヒープが空になるまで以下の２つのステップを繰り返す。

　ステップ１　最上位のｈ(1)を取り出す。
　ステップ２　残りのヒープｈ(2),ｈ(3),...,ｈ(n)をヒープに再構成する。
　　　　　 再構成は、以下のa), b) にしたがって行なう。
　　　　　　a) ｈ(1)の位置にｈ(n)を移動する。もとのｈ(n)は削除する。
　　　　　  b) ｈ(1)の位置からshiftdown操作を行なう。
　　　　　　　 shiftdown操作： ｈ(i) < max(ｈ(2i), ｈ(2i+1))のとき、
　　　　　　　　　　　　　　　 ｈ(2i)とｈ(2i+1)の大きい方をｈ(i)と交換する。
                               交換したところから、同様な操作を繰り返す。

　shiftdown操作の例を以下に示す。

初期状態：
　　　　　　　　　　　　　　 ８４
　　　　　　　　　┌─────┴─────┐
　　　　　　　　 ７３ 　　　　　　　　　 ６６
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ２２ 　　　　　 ３７ 　 １１ 　　　　　 ４９
　　┌──┴──┐
　　６

状態２：初期状態においてｈ(1)である８４を取り出し、ｈ(n)である６をｈ(1)の位置に移動する。

　　　　　　　　　　　　　　　６　　　　　　　　───＞８４
　　　　　　　　　┌─────┴─────┐
　　　　　　　   ７３ 　　　　　　　　　 ６６
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ２２ 　　　　　 ３７ 　 １１ 　　　　　 ４９
　　┌──┴──┐
　　
ｈ(1)の位置（６）からshiftdown操作を行なう。

　　　　　　　　　　　　　　 ７３ 　　　　　　　───＞８４
　　　　　　　　　┌─────┴─────┐
　　　　　　　　　６　　　　　　　　　　 ６６
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ２２ 　　　　　 ３７ 　 １１ 　　　　　 ４９


　　　　　　　　　　　　　　　７３　　　　　　　───＞８４
　　　　　　　　　┌─────┴─────┐
　　　　　　　　 ３７ 　　　　　　　　　 ６６
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ２２ 　　　　　　６　　 １１ 　　　　　 ４９


状態３：ｈ(1)である７３を取り去り、ｈ(n)である４９をｈ(1)の位置に移動する。

　　　　　　　　　　　　　　 ４９ 　　　　　　　───＞　７３　８４
　　　　　　　　　┌─────┴─────┐
　　　　　　　　　６　　　　　　　　　　 ６６
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ２２ 　　　　　 ３７ 　 １１ 

　ｈ(1)からshiftdown操作を行なう。

　　　　　　　　　　　　　　 ６６ 　　　　　　　───＞　７３　８４
　　　　　　　　　┌─────┴─────┐
　　　　　　　　　６　　　　　　　　　　 ４９
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ２２ 　　　　　 ３７ 　 １１　　　　　
　

状態４：６６を取り除き、１１をｈ(1)位置に移動し、shiftdown操作を行なう。

　　　　　　　　　　　　　　 ４９　　　　　　　───＞　６６　７３　８４
　　　　　　　　　┌─────┴─────┐
　　　　　　　　　６　　　　　　　　　　 １１
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ２２ 　　　　　 ３７


状態５：以下同様な操作を繰り返す。

  　　　　　　　　　　　　　 ３７　　　　　　　───＞　４９　６６　７３　８４
　　　　　　　　　┌─────┴─────┐
    　　　　　　　６　　　　　　　　　　 １１
　　　　　┌───┴───┐　　　┌───┴───┐
  　　　 ２２


状態６：

　　　　　　　　　 ２２ 　　　　　　　───＞　３７　４９　６６　７３　８４
　　　　┌─────┴─────┐
　　　　６　　　　　　　　　　 １１


状態７：

　　　　　　　　　 １１ 　　　　───＞　２２　３７　４９　６６　７３　８４
　　　　┌─────┴─────┐
　　　　６　


状態８：

　　　　　　　　　　６　　───＞　１１　２２　３７　４９　６６　７３　８４
　　　　┌─────┴─────┐

よって、取り除かれたデータは並べ換えが済んでいる。

　次に、最初のヒープを構成する方法について述べる。

ステップ１	任意の２分木を与える。この２分木の各頂点のデータの値をそれぞれ ｈ(1)，ｈ(2)，ｈ(3)，...をする。
ステップ２	この２分木で、枝が１本も出ていない頂点、つまり 　　　　　　ｈ(k)，ｈ(k+1)，...，ｈ(n)　（k=[n/2]+1） は、下位にデータを持たないため、ヒープの条件が満足されていると解釈できる。
ステップ３	残りの頂点をｈ(k-1),ｈ(k-2),...,ｈ(1)の順にとりあげ、その頂点を下位の部分木の根（ｈ(1)）とみたてヒープを構成していく。その際には、前記のshiftdown操作を使う。

---

ヒープ生成の例

初期状態：
　　　　　　　　　　　　　　 ２１
　　　　　　　　　┌─────┴─────┐
　　　　　　　　 ５３ 　　　　　　　　　 １２
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ４６ 　　　　　 ８７ 　 ５９ 　　　　　 ４０
　　┌──┴──┐
　 ７０


状態２：初期状態において７０，４０，５９，８７は下位にデータを持たな
	いので、ヒープの条件を満足していると考えられる。まず、４６を
	２分木の根とみたてshiftdown操作を行なう。

　　　　　　　　　　　　　　 ２１
　　　　　　　　　┌─────┴─────┐
　　　　　　　　 ５３ 　　　　　　　　　 １２
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ７０ 　　　　　 ８７ 　 ５９ 　　　　　 ４０
　　┌──┴──┐
　 ４６


状態３：状態２において７０，８７，５９，４０，４６は、ヒープの条件を
	満足していると考えられる。次に１２を２分木の根とみたて
	shiftdown操作を行なう。

　　　　　　　　　　　　　　 ２１
　　　　　　　　　┌─────┴─────┐
　　　　　　　　 ５３ 　　　　　　　　　 ５９
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ７０ 　　　　　 ８７ 　 １２ 　　　　　 ４０
　　┌──┴──┐
　 ４６


状態４：状態３において５９，７０，８７，１２，４０，４６は、ヒープの
	条件を満足していると考えられる。次に５３を２分木の根とみたて
	shiftdown操作を行なう。

　　　　　　　　　　　　　　 ２１
　　　　　　　　　┌─────┴─────┐
　　　　　　　　 ８７ 　　　　　　　　　 ５９
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ７０ 　　　　　 ５３ 　 １２ 　　　　　 ４０
　　┌──┴──┐
　 ４６


状態５：状態４において８７，５９，７０，５３，１２，４０，４６は、ヒー
	プの条件を満足していると考えられる。次に２１についてshiftdown
	操作を行なう。

　　　　　　　　　　　　　　 ８７
　　　　　　　　　┌─────┴─────┐
　　　　　　　　 ７０ 　　　　　　　　　 ５９
　　　　　┌───┴───┐　　　┌───┴───┐
　　　　 ４６ 　　　　　 ５３ 　 １２ 　　　　　 ４０
　　┌──┴──┐
　 ２１

よって、任意に与えた２分木に対して、ヒープが構成できた。

　上記で説明した考えをもとに、データの並べ換えを行なう。実際に計算機で行なう場合、２分木を表現することは面倒なことである。そこで、今回は配列を工夫し２分木にみたてておこなう。下記のような配列を考えてみよう。

便宜的に、配列の区切りを入れている所と入れていない所がある。これは、２分木の階層を明らかにするためである。上記配列は、下記の２分木を表現していることを理解していただきたい。

　　　　　　　　　　　　　　　　　　 ｈ(1)
　　　　　　　　　　　　　　　　　　　│
　　　　　　　　　　┌────────┴────────┐
　　　　　　　　　 ｈ(2)　　　　　　　　　　　　　　　 ｈ(3)
　　　　┌─────┴─────┐　　　　　┌─────┴─────┐
　　　 ｈ(4)　　　　　　　　　 ｈ(5)　　　 ｈ(6)　　　　　　　　　 ｈ(7)
　┌──┴──┐　　　　　┌──┴──┐
 ｈ(8)　　　 ｈ(9)　　　 ｈ(10)

　アルゴリズムの進行とともにヒープが縮小するため、配列の後尾が空となる。そこで、ヒープから取り出したデータを配列の後ろから順に詰めて行くことにより、ソートが完了した時点で、配列内にデータが並べ替わっていることになる。

---

配列の場合の例

（１）初期ヒープの生成

初期データ：	21 53 12 46 87 59 40 70
状態２：	初期状態において７０，４０，５９，８７は下位にデータを持たないので、ヒープの条件を満足していると考えられる。まず、４６を２分木の根とみたてshiftdown操作を行なう。 21 53 12 70 87 59 40 46
状態３：	状態２において７０，８７，５９，４０，４６は、ヒープの条件を満足していると考えられる。次に１２を２分木の根とみたてshiftdown操作を行なう。 21 53 59 70 87 12 40 46
状態４：	状態３において５９，７０，８７，１２，４０，４６は、ヒープの条件を満足していると考えられる。次に５３を２分木の根とみたてshiftdown操作を行なう。 21 87 59 70 53 12 40 46
状態５：	状態４において８７，５９，７０，５３，１２，４０，４６は、ヒープの条件を満足していると考えられる。次に２１を２分木の根とみたてshiftdown操作を行なう。 87 70 59 46 53 12 40 21

---

（２）ソート

初期状態：	87 70 59 46 53 12 40 21
状態２：	先頭の８７（ｈ(1)）を取り出しす。　２１（ｈ(k)）を２分木の根（ｈ(1)）に移動し、shiftdown操作を行なう。　取り出した８７は配列の最後に格納する。 70 53 59 46 21 12 40 87
状態３：	先頭の７０（ｈ(1)）を取り出しす。４０を２分木の根（ｈ(1)）に移動し、shiftdown操作を行なう。　取り出した７０は配列の最後から２番目にに格納する。 59 53 40 46 21 12 70 87
状態４：	先頭の５９（ｈ(1)）を取り出す。１２を２分木の根（ｈ(1)）に移動し、shiftdown操作を行なう。　取り出した５９は配列の最後から３番目に格納する。 53 46 40 12 21 59 70 87
状態５：	以下同様な操作を繰り返す。 46 21 40 12 53 59 70 87
状態６：	39 20 12 46 53 59 70 87
状態７：	21 12 40 46 53 59 70 87
状態８：	12 21 40 46 53 59 70 87

　上記考えをプログラムすると、プログラム６−５のようになる。

---

/*   1 */  /*  Program 6-5   */
/*   2 */  /*   Heap Sort   */
/*   3 */
/*   4 */  #include<stdio.h>
/*   5 */  #define  MaxNumber  100
/*   6 */  #define INIT  1984
/*   7 */
/*   8 */  void HeapSort( int data[], int n );
/*   9 */  void Shiftdown(int data[], int top, int bottom);
/*  10 */  void Outputdata( int data[], int n );
/*  11 */  void Makedata( int data[], int n );
/*  12 */  int rnd(void);
/*  13 */
/*  14 */
/*  15 */
/*  16 */  main()
/*  17 */  {
/*  18 */       int data[MaxNumber], i;
/*  19 */       
/*  20 */       Makedata(data, MaxNumber);
/*  21 */       HeapSort(data, MaxNumber-1);
/*  22 */       Outputdata(data, MaxNumber);
/*  23 */  }
/*  24 */
/*  25 */  void HeapSort( int data[], int n )
/*  26 */  {
/*  27 */       int top, bottom, tmp;
/*  28 */
/*  29 */       bottom = n/2 +1;
/*  30 */       top = n;
/*  31 */       while ( bottom > 0 )
/*  32 */       {
/*  33 */               bottom--;
/*  34 */               Shiftdown( data, top, bottom );
/*  35 */       }
/*  36 */       while ( top > 0 )
/*  37 */       {
/*  38 */               tmp = data[0];
/*  39 */               data[0] = data[top];
/*  40 */               data[top] = tmp;
/*  41 */               top--;
/*  42 */               Shiftdown( data, top, bottom );
/*  43 */       }
/*  44 */  }
/*  45 */
/*  46 */  void Shiftdown(int data[], int top, int bottom)
/*  47 */  {
/*  48 */       int i, tmp;
/*  49 */       
/*  50 */       i = 2 * bottom;
/*  51 */       while( i <= top )
/*  52 */       {
/*  53 */               if( i < top && data[i+1]>data[i] )  i++;
/*  54 */               if( data[bottom]>=data[i] )  break;
/*  55 */               tmp = data[bottom];
/*  56 */               data[bottom] = data[i];
/*  57 */               data[i] = tmp;
/*  58 */               bottom = i;
/*  59 */               i = 2 * bottom;
/*  60 */       }
/*  61 */  }
/*  62 */
/*  63 */  void Outputdata(int data[], int n)
/*  64 */  {
/*  65 */       int i;
/*  66 */       
/*  67 */       for (i=0; i < n; i++)
/*  68 */       {
/*  69 */                   printf("%8d", data[i]);
/*  70 */       }
/*  71 */  }
/*  72 */
/*  73 */  void Makedata( int data[], int n)
/*  74 */  {
/*  75 */       int i;
/*  76 */
/*  77 */       for (i=0; i < n; i++)
/*  78 */               data[i] = rnd();
/*  79 */  }
/*  80 */
/*  81 */  int rnd(void)
/*  82 */  {
/*  83 */       static unsigned long mod = INIT;
/*  84 */
/*  85 */       mod = (23 * mod) % 32749;
/*  86 */       return mod;
/*  87 */  }

---

　３１−３５で初期のヒープを作成し、３６−４３でヒープの再構成を行なっている。

　ヒープソートの計算時間量は、Ｏ（ｎ ｌｏｇ ｎ）である。簡単に、理由を述べる。主に関数shiftdown内の入れ換えの回数に着目してやればよい。つまり、５５−５７の実行回数である。２分木の根から順に、下位の部分木の頂点にあるデータと比較するため、１回のshiftdown操作では、ｌｏｇ（ｎ）回（ｌｏｇとは対数関数であり、この場合２分木であるため対数の底を２として考えている。ｎはデータの個数である。）比較を行なっていることになる。

　関数shiftdownの呼ばれる回数は、データの個数ｎに比例している。そのため、ｎ＊ｌｏｇ（ｎ）が得られる。基本的な考え方は以上の通りである。

　詳細は、演習問題としよう。

　ヒープソートは、クイックソートに比べて平均約２倍のスピードを要する。しかしながら、ヒープソートは、どのような配置のデータにも常にＯ（ｎ ｌｏｇ ｎ）で処理がなされ、外部記憶装置内のデータにも適用可能なことから、利用度の高いアルゴリズムであるといえる。

---

（３）シェルソート

　シェルソートは、分割法を適用したひとつの方法である。基本的な考え方は、与えられたデータをいくつかのブロックに分割し、そのブロックに対し単純挿入法を行なうもである。データをいくつかのブロックに分割し大ざっぱな並べ替えを繰り返しながら、最終的には全データに対して並べ替えをする。このように分割することによって、データの入れ替えの回数を少なくすることを、Ｄ．Ｓｈｅｌｌによって考えられ、シェルソートの名前が付いた。

　例を用いて、シェルソートの動作を示そう。

入力データ	45　 56　 13　 43　 95　 18　 7　 68
ステップ１	分割の幅をｓｋｉｐ＝４とし、上記データをいくつかのブロックに分割する。 　　　　45　 56　 13　 43　 95　 18　 7　 68 　　　　↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ 　　　 B1 　B2 　B3 　B4 　B1 　B2 　B3 　B4 ←便宜上ブロックに名前を付けた このブロック内で並べ替えをおこなう。 　　　　Ｂ１ブロック　　 45 95 　→ 45 95 　　　　Ｂ２ブロック　　 56 18 　→ 18 56 　　　　Ｂ３ブロック　　 13 7 　→ 7 13 　　　　Ｂ４ブロック　　 43 68 　→ 43 68 よって、 　　　　45　 18　 7　 43　 95　 56　 13　 68 となる。
ステップ２	分割の幅を１／２にする。ｓｋｉｐ＝２としてブロックに分割する。 　　　　45　 18　 7　 43　 95　 56　 13　 68 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ 　　　 B1 　B2 　B1 　B2 　B1 　B2 　B1 　B2 このブロック内で並べ替えを行なう。 　　　　Ｂ１ブロック　　45 7 95 13 　→ 7 13 45 95 　　　　Ｂ２ブロック　　18 43 56 68 　→ 18 43 56 68 よって、 7 18 13 43 45 56 95 68 となる。
ステップ３	分割の幅をさらに１／２にする。ｓｋｉｐ＝１となり、全データを一つのブロックとして考える。よって、 7 13 18 43 45 56 68 95 となり、並べ替えが完了する。

　上記分割の幅の取り方は任意でよいが、ステップを増すごとに幅が減少していなければならない。最後のステップでは、ｓｋｉｐ＝１として必ず全データを一つのブロックとして並べ替えを行なわなければならない。

　シェルソートのプログラムを以下に示そう。

---

プログラム６−６

/*   1 */  /*  Program 6-6   */
/*   2 */  /*   Shell Sort   */
/*   3 */
/*   4 */  #include<stdio.h>
/*   5 */  #define  MaxNumber  100
/*   6 */  #define INIT  1984
/*   7 */
/*   8 */  void ShellSort(int data[], int n);
/*   9 */  void SimpleInsertion( int data[], int skip, int n );
/*  10 */  void Outputdata( int data[], int n );
/*  11 */  void Makedata( int data[], int n );
/*  12 */  int rnd(void);
/*  13 */
/*  14 */
/*  15 */
/*  16 */  main()
/*  17 */  {
/*  18 */       int data[MaxNumber], i;
/*  19 */       
/*  20 */       Makedata(data, MaxNumber);
/*  21 */       ShellSort(data, MaxNumber);
/*  22 */       Outputdata(data, MaxNumber);
/*  23 */  }
/*  24 */
/*  25 */  void ShellSort(int data[], int n)
/*  26 */  {
/*  27 */       int i, skip;
/*  28 */
/*  29 */       skip = n / 2;
/*  30 */       while( skip > 0 )
/*  31 */       {
/*  32 */               SimpleInsertion( data, skip, n );
/*  33 */               skip = skip / 2;
/*  34 */       }
/*  35 */  }
/*  36 */
/*  37 */  void SimpleInsertion(int data[], int skip, int n)
/*  38 */  {
/*  39 */       int tmp, i, j;
/*  40 */
/*  41 */       for (i=skip; i < n; i=i+skip)
/*  42 */               for (j=i-skip; j >= 0; j=j-skip)
/*  43 */                       if(data[j] > data[j+skip])
/*  44 */                       {
/*  45 */                               tmp = data[j];
/*  46 */                               data[j] = data[j+skip];
/*  47 */                               data[j+skip] = tmp;
/*  48 */                       }
/*  49 */  }
/*  50 */
/*  51 */  void Outputdata(int data[], int n)
/*  52 */  {
/*  53 */       int i;
/*  54 */       
/*  55 */       for (i=0; i < n; i++)
/*  56 */       {
/*  57 */                   printf("%8d", data[i]);
/*  58 */       }
/*  59 */  }
/*  60 */
/*  61 */  void Makedata( int data[], int n)
/*  62 */  {
/*  63 */       int i;
/*  64 */
/*  65 */       for (i=0; i < n; i++)
/*  66 */               data[i] = rnd();
/*  67 */  }
/*  68 */
/*  69 */  int rnd(void)
/*  70 */  {
/*  71 */       static unsigned long mod = INIT;
/*  72 */
/*  73 */       mod = (23 * mod) % 32749;
/*  74 */       return mod;
/*  75 */  }

---

　３７〜４９は、単純挿入法の関数である。プログラム６−３で紹介した関数と別なものをここでは紹介した。一見バブルソートに外観が似ているが、基本的な考え方は単純挿入法であることに注意しよう。ただし、変数ｓｋｉｐを用いて１次元的なデータをｓｋｉｐ個おきに取っていくことによって、ブロックに分割しているように扱っている。 　２５〜３５では、分割の幅をデータの個数の半分を初期値として、幅が１になる値を１／２にして単純挿入法を繰り返している。

　上記シェルソートでは、分割の幅を１／２にして求めているが、任意でよいが、なるべく互いに素（割り切れない）の数を選ぶとよい。この幅の取り方によってデータの入れ替え回数が変わることが知られている。

　Ｄ．Ｅ．Ｋｎｕｔｈは、以下のような数列で分割の幅を採用すると効率がよいことを示した。

１、４、１３、４０、１２１、．．

一般的に、Ｓi+1 ＝ ３＊Ｓi ＋１, Ｓ1＝１　で得られる数列を逆順にとるものとする。これらの数値は、互いに素ではないが、より効率的であることが知られている。

　プログラム６−５−２は、上記Knuthが推奨する数列で得られた数値を分割幅に採用した例である。

---

プログラム６−６−２

/*   1 */  /*  Program 6-6-2   */
/*   2 */  /*   Shell Sort( Knuth Version )   */
/*   3 */
/*   4 */  #include<stdio.h>
/*   5 */  #define  MaxNumber  100
/*   6 */  #define INIT  1984
/*   7 */
/*   8 */  void ShellSort(int data[], int n);
/*   9 */  void SimpleInsertion( int data[], int skip, int n );
/*  10 */  void Outputdata( int data[], int n );
/*  11 */  void Makedata( int data[], int n );
/*  12 */  int rnd(void);
/*  13 */
/*  14 */
/*  15 */
/*  16 */  main()
/*  17 */  {
/*  18 */       int data[MaxNumber], i;
/*  19 */       
/*  20 */       Makedata(data, MaxNumber);
/*  21 */       ShellSort(data, MaxNumber);
/*  22 */       Outputdata(data, MaxNumber);
/*  23 */  }
/*  24 */
/*  25 */  void ShellSort(int data[], int n)
/*  26 */  {
/*  27 */       int i, skip[] = {121,40,13,4,1};
/*  28 */
/*  29 */       for ( i=0; i < 5; i++ )
/*  30 */               SimpleInsertion( data, skip[i], n );
/*  31 */  }
/*  32 */
/*  33 */  void SimpleInsertion(int data[], int skip, int n)
/*  34 */  {
/*  35 */       int tmp, i, j;
/*  36 */
/*  37 */       for (i=skip; i < n; i=i+skip)
/*  38 */               for (j=i-skip; j >= 0; j=j-skip)
/*  39 */                       if(data[j] > data[j+skip])
/*  40 */                       {
/*  41 */                               tmp = data[j];
/*  42 */                               data[j] = data[j+skip];
/*  43 */                               data[j+skip] = tmp;
/*  44 */                       }
/*  45 */  }
/*  46 */
/*  47 */  void Outputdata(int data[], int n)
/*  48 */  {
/*  49 */       int i;
/*  50 */       
/*  51 */       for (i=0; i < n; i++)
/*  52 */       {
/*  53 */                   printf("%8d", data[i]);
/*  54 */       }
/*  55 */  }
/*  56 */
/*  57 */  void Makedata( int data[], int n)
/*  58 */  {
/*  59 */       int i;
/*  60 */
/*  61 */       for (i=0; i < n; i++)
/*  62 */               data[i] = rnd();
/*  63 */  }
/*  64 */
/*  65 */  int rnd(void)
/*  66 */  {
/*  67 */       static unsigned long mod = INIT;
/*  68 */
/*  69 */       mod = (23 * mod) % 32749;
/*  70 */       return mod;
/*  71 */  }

---

　シェルソートの計算時間量は、分割の幅の取り方によりＯ（ｎ＾1.2）からＯ（ｎ＾2）であることが、知られている。証明については、難しいため省略する。

　さらに、単純挿入法の関数をプログラム６−３で紹介したものと置き換えた例を以下に示そう。

---

プログラム６−６−３

/*   1 */  /*  Program 6-6-3   */
/*   2 */  /*   Shell Sort   */
/*   3 */
/*   4 */  #include<stdio.h>
/*   5 */  #define  MaxNumber  200
/*   6 */  #define INIT  1984
/*   7 */
/*   8 */  void ShellSort(int data[], int n);
/*   9 */  void SimpleInsertion2( int data[], int skip, int n );
/*  10 */  void Outputdata( int data[], int n );
/*  11 */  void Makedata( int data[], int n );
/*  12 */  int rnd(void);
/*  13 */
/*  14 */
/*  15 */
/*  16 */  main()
/*  17 */  {
/*  18 */       int data[MaxNumber], i;
/*  19 */       
/*  20 */       Makedata(data, MaxNumber);
/*  21 */       ShellSort(data, MaxNumber);
/*  22 */       Outputdata(data, MaxNumber);
/*  23 */  }
/*  24 */
/*  25 */  void ShellSort(int data[], int n)
/*  26 */  {
/*  27 */       int i, skip[] = {121,40,13,4,1};
/*  28 */
/*  29 */       for ( i=0; i < 5; i++ )
/*  30 */               SimpleInsertion2( data, skip[i], n );
/*  31 */  }
/*  32 */
/*  33 */  void SimpleInsertion2(int data[], int skip, int n)
/*  34 */  {
/*  35 */       int tmp, i, j;
/*  36 */
/*  37 */       for( j=skip; j < n; j++ )
/*  38 */       {
/*  39 */               i = j - skip;
/*  40 */               tmp = data[j];
/*  41 */               while( (i>=0) && (tmp<data[i]) )
/*  42 */               {
/*  43 */                       data[i+skip] = data[i];
/*  44 */                       i = i - skip;
/*  45 */               }
/*  46 */               data[i+skip] = tmp;
/*  47 */       }
/*  48 */  }
/*  49 */
/*  50 */  void Outputdata(int data[], int n)
/*  51 */  {
/*  52 */       int i;
/*  53 */       
/*  54 */       for (i=0; i < n; i++)
/*  55 */       {
/*  56 */                   printf("%8d", data[i]);
/*  57 */       }
/*  58 */  }
/*  59 */
/*  60 */  void Makedata( int data[], int n)
/*  61 */  {
/*  62 */       int i;
/*  63 */
/*  64 */       for (i=0; i < n; i++)
/*  65 */               data[i] = rnd();
/*  66 */  }
/*  67 */
/*  68 */  int rnd(void)
/*  69 */  {
/*  70 */       static unsigned long mod = INIT;
/*  71 */
/*  72 */       mod = (23 * mod) % 32749;
/*  73 */       return mod;
/*  74 */  }

---

練習問題

　分割幅の違いによるデータの入れ替え回数の違いを、実際にカウンターをプログラム内に埋め込んで、確かめてみよう。

　分割幅は、以下の３つの場合について行なう。

（１）　分割を行なわず、初めから ｓｋｉｐ＝１として行なう。
（２）　ｓｋｉｐ＝２／ｎ，４／ｎ，８／ｎ，．．．１の順で分割を行なう。
（３）　ｓｋｉｐ＝．．．，１２１，４０，１３，４，１の順で行なう。

　カウンタは、グローバルに変数宣言し、例えばプログラム６−５についていえば、

/*  37 */  void SimpleInsertion(int data[], int skip, int n)
/*  38 */  {
/*  39 */       int tmp, i, j;
/*  40 */
/*  41 */       for (i=skip; i < n; i=i+skip)
/*  42 */               for (j=i-skip; j >= 0; j=j-skip)
/*  43 */                       if(data[j] > data[j+skip])
/*  44 */                       {
/*  45 */                               tmp = data[j];
/*  46 */                               data[j] = data[j+skip];
/*  47 */                               data[j+skip] = tmp;
                                        count = count + 3;
/*  48 */                       }
/*  49 */  }
/*  50 */

のように、４７と４８の間にデータの入れ替え回数を計算する命令を挿入してやればよい。ただし初期値として count=0 がセットされていなければならない。

---

（４）　マージソート

　マージソートの基本的な考え方は、あらかじめ並べ替えが完了している２つのデータを１つに合併する操作を組織的に適用することによって、最終的にソートされたデータを得るものである。本来は、磁気テープによる外部ソートを行なう有力な方法として発達してきたが、ここでは内部ソートとして考えてみよう。以下簡単のため、データの個数を２のべき乗と仮定する。基本原理（マージ操作）を例によって示す。２本のソート済みの磁気テープが存在しているとする。

	         13   43   45   56    ← テープ１
	          7   18   68   95    ← テープ２

これらを、マージしよう。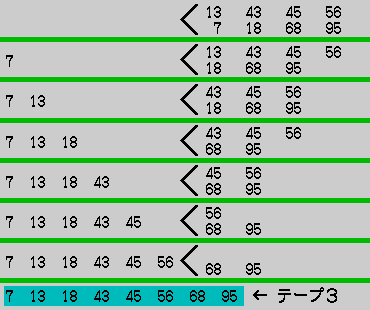

　この場合、磁気テープを余分に１本必要とすることに注意。

　上記基本原理を、１次元配列のデータに対して行なうために、データを２分割し、疑似的に２本の磁気テープを構成する。例を用いて、（内部的な）マージソートの動作を示そう。

入力データ	ｎ＝２＾３個とする。 　　　　　45　56　43　13　95　18　 7　68
ステップ１	上記データを２つに分割する。 　　　　( 45　56　43　13 )　と　( 95　18　 7　68 )　の２組のデータに分ける。 　　２組の各データをさらに分割する。 　　　　( 45　56 )　と　( 43　13 )　と　( 95　18 )　と　( 7　68 ) 　　上記操作を２つのデータの組になるまで、繰り返す。
ステップ２	２つのデータの各組に対し、マージ操作を行なう。よって、 　　　　( 45　56 ) 　と　( 13　43 )　と　( 18　95 )　と　( 7　68 ) さらに、マージ操作を繰り返す。よって 　　　　( 13　43　45　56 ) 　と　( 7　18　68　95 ) となる。さらに、マージ操作を行なう。よって、 　　　　　 7　13　18　43　45　56　68　95 となる。

　マージソートのプログラムを以下に示す。

---

プログラム６−７

/*   1 */  /*  Program 6-7   */
/*   2 */  /*   Merge Sort   */
/*   3 */
/*   4 */  #include<stdio.h>
/*   5 */  #define  MaxNumber  128
/*   6 */  #define INIT  1984
/*   7 */
/*   8 */  void MergeSort( int data[], int top, int bottom );
/*   9 */  void Merge( int data[], int l, int m );
/*  10 */  void Outputdata( int data[], int n );
/*  11 */  void Makedata( int data[], int n );
/*  12 */  int rnd(void);
/*  13 */
/*  14 */
/*  15 */
/*  16 */  main()
/*  17 */  {
/*  18 */       int data[MaxNumber+1], i;
/*  19 */       
/*  20 */       Makedata(data, MaxNumber);
/*  21 */       MergeSort(data, 1, MaxNumber);
/*  22 */       Outputdata(data, MaxNumber);
/*  23 */  }
/*  24 */
/*  25 */  void MergeSort( int data[], int left, int right )
/*  26 */  {
/*  27 */       int mid;
/*  28 */
/*  29 */       if( left < right )
/*  30 */       {
/*  31 */               mid = (right - left + 1) / 2;
/*  32 */               MergeSort( data, left, left+mid-1 );
/*  33 */               MergeSort( data, left+mid, right );
/*  34 */               Merge( data, left, left+mid );
/*  35 */       }
/*  36 */  }
/*  37 */
/*  38 */  void Merge( int data[], int l, int m )
/*  39 */  {
/*  40 */       int tmp[MaxNumber+1], h, i, j, k, r;
/*  41 */       
/*  42 */       i = l;
/*  43 */       j = m;
/*  44 */       r = 2*m-l;
/*  45 */       k = l;
/*  46 */       while( (i<m) && (j<r) )
/*  47 */       {
/*  48 */               if( data[i]<data[j] )
/*  49 */               {
/*  50 */                       tmp[k] = data[i];
/*  51 */                       i++;
/*  52 */               }
/*  53 */               else
/*  54 */               {
/*  55 */                       tmp[k] = data[j];
/*  56 */                       j++;
/*  57 */               }
/*  58 */               k++;
/*  59 */       }
/*  60 */       if( i<m )
/*  61 */               for( h=i; h<m; h++ )
/*  62 */               {
/*  63 */                       tmp[k] = data[h];
/*  64 */                       k++;
/*  65 */               }
/*  66 */       if( j<r )
/*  67 */               for( h=j; h<r; h++ )
/*  68 */               {
/*  69 */                       tmp[k] = data[h];
/*  70 */                       k++;
/*  71 */               }
/*  72 */       for( h=l; h<r; h++ )
/*  73 */               data[h] = tmp[h];
/*  74 */  }    
/*  75 */
/*  76 */  void Outputdata(int data[], int n)
/*  77 */  {
/*  78 */       int i;
/*  79 */       
/*  80 */       for (i=1; i <= n; i++)
/*  81 */       {
/*  82 */                   printf("%8d", data[i]);
/*  83 */       }
/*  84 */       printf("\n");
/*  85 */  }
/*  86 */
/*  87 */  void Makedata( int data[], int n)
/*  88 */  {
/*  89 */       int i;
/*  90 */
/*  91 */       for (i=1; i <= n; i++)
/*  92 */               data[i] = rnd();
/*  93 */  }
/*  94 */
/*  95 */  int rnd(void)
/*  96 */  {
/*  97 */       static unsigned long mod = INIT;
/*  98 */
/*  99 */       mod = (23 * mod) % 32749;
/* 100 */       return mod;
/* 101 */  }

---

　マージソートの計算時間量は、ｎ＊ｌｏｇ（ｎ）である。データが２個になるまでデータの２分割を繰り返していく。この分割は、ｌｏｇ（ｎ）回行なわれる。各ステージでは、並べ替えが行なわれ、その計算量はＯ（ｎ）である。よって、全体でｎ＊ｌｏｇ（ｎ）となる。

---

演習問題

　関数MergeSort内で再帰的にMergeSortを呼んでいる。大量のデータを処理したり再帰のもぐる段階が増すと、再帰的な関数は一般的に効率が悪い。そこで、再帰を用いないでMergeSortプログロムを書き換えよ。

---

６．４　効率のよいソートプログラムとは？

　データの並べ替えを行なうにも、これまで紹介してきたようにいくつものアルゴリズムが存在する。そこで我々は、用途によってアルゴリズムを使い分けなければならない。処理スピードが速い方がよいとは思うが、たった１度だけのデータの並べ替えのために、複雑なプログラムをわざわざ作ることもない。エラーを訂正しているうちには、データの並べ替えが終了してしまう。また、頻繁に大量のデータを並べ替えするような場合は、多少プログラムの作成に時間をかけても、計算の処理時間を考えると複雑なプログラムを作成する価値はある。

　そこで、データの大きさと計算時間との関係を知ることは、重要なことである。さらに、扱うデータの個数や用途により、採用するアルゴリズムを交えることも必要である。

　Ｎｏ．１７の最後に提示した上級演習問題を、Ｎｏ．１７−１９で示したすべてのプログラムについて行なってみることをすすめる。そして、実行スピードの限界となるデータの個数を断定せよ。