7.グラフ的データ構造
7.1 リスト構造
7.1.1 線形リスト
-
線形リストは、出発点に最初のデータの格納位置を指すポインタが格納されて、その先にはデータと次の格納位置が組となって次々とつながっている。
例7-1 入力したデータの順につながった線形リストを作成し,先頭から順に格納データを出力せよ.
プログラム7-1
/* 1 */ /* Example 7-1 */ /* 2 */ /* Making List */ /* 3 */ /* 4 */ #include<stdio.h> /* 5 */ /* 6 */ struct Node_type{ /* 7 */ int data; /* 8 */ struct Node_type *next; /* 9 */ }; /* 10 */ /* 11 */ struct Node_type *getmemory(void); /* 12 */ void Output_List(struct Node_type *p); /* 13 */ /* 14 */ main() /* 15 */ { /* 16 */ struct Node_type *head, *current, *previous; /* 17 */ /* 18 */ head = getmemory(); /* 19 */ scanf("%d", &head->data); /* 20 */ previous = head; /* 21 */ head->next = NULL; /* 22 */ /* 23 */ while( current=getmemory(), scanf("%d", ¤t->data) != EOF ) /* 24 */ { /* 25 */ previous->next = current; /* 26 */ previous = current; /* 27 */ } /* 28 */ current->next = NULL; /* 29 */ /* 30 */ Output_List(head); /* 31 */ printf("\n"); /* 32 */ } /* 33 */ /* 34 */ struct Node_type *getmemory(void) /* 35 */ { /* 36 */ return( (struct Node_type *)malloc(sizeof(struct Node_type)) ); /* 37 */ } /* 38 */ /* 39 */ void Output_List(struct Node_type *p) /* 40 */ { /* 41 */ while( p != NULL ) /* 42 */ { /* 43 */ printf("%8d", p->data); /* 44 */ p = p->next; /* 45 */ } /* 46 */ }解説
-
6〜9: ノードの型の定義を行っている.構成要素は,整数型のデータとノードを指すポインタである. 18〜21: 初期設定を行う.23〜27のループをきれいに作るために最初のノードへのデータの格納を行う. 23〜27: データを読み込み,新しいノードの領域を確保し,それをリストの末尾につなげる.この操作を,データがなくなるまで繰り返す.新しく確保したノードの位置はcurrentに格納される.ポインタをつなぐために,一つ前に確保した領域の位置をpreviousとして覚えておく. 34〜37: ノードの領域を確保するための関数である.この関数が呼ばれる度に,新しい領域がメモリ上に確保される. 39〜46: リストを順にたどりながら,格納されているデータの出力を行う.
プログラム7-1の 18〜27行をすっきりさせたプログラムを次に示す.プログラム7-1-2
/* 1 */ /* Example 7-1-2 */ /* 2 */ /* Making List */ /* 3 */ /* 4 */ #include<stdio.h> /* 5 */ /* 6 */ struct Node_type{ /* 7 */ int data; /* 8 */ struct Node_type *next; /* 9 */ }; /* 10 */ /* 11 */ struct Node_type *getmemory(void); /* 12 */ void Output_List(struct Node_type *p); /* 13 */ /* 14 */ main() /* 15 */ { /* 16 */ struct Node_type *head, *current, *previous; /* 17 */ int temp; /* 18 */ /* 19 */ previous = NULL; /* 20 */ /* 21 */ while( scanf("%d", &temp) != EOF ) /* 22 */ { /* 23 */ current=getmemory(); /* 24 */ current->data = temp; /* 25 */ if( previous == NULL ) /* 26 */ head = current; /* 27 */ else /* 28 */ previous->next = current; /* 29 */ previous = current; /* 30 */ } /* 31 */ current->next = NULL; /* 32 */ /* 33 */ Output_List(head); /* 34 */ printf("\n"); /* 35 */ } /* 36 */ /* 37 */ struct Node_type *getmemory(void) /* 38 */ { /* 39 */ return( (struct Node_type *)malloc(sizeof(struct Node_type)) ); /* 40 */ } /* 41 */ /* 42 */ void Output_List(struct Node_type *p) /* 43 */ { /* 44 */ while( p != NULL ) /* 45 */ { /* 46 */ printf("%8d", p->data); /* 47 */ p = p->next; /* 48 */ } /* 49 */ }例7-2 入力したデータの逆順につながった線形リストを作成し,先頭から 順に格納データを出力せよ.
プログラム7-2
/* 1 */ /* Example 7-2 */ /* 2 */ /* Making List (Reversal oedre) */ /* 3 */ /* 4 */ #include<stdio.h> /* 5 */ /* 6 */ struct Node_type{ /* 7 */ int data; /* 8 */ struct Node_type *next; /* 9 */ }; /* 10 */ /* 11 */ struct Node_type *getmemory(void); /* 12 */ void Output_List(struct Node_type *p); /* 13 */ /* 14 */ main() /* 15 */ { /* 16 */ struct Node_type *head, *previous; /* 17 */ /* 18 */ previous = NULL; /* 19 */ /* 20 */ while( head=getmemory(), scanf("%d", &head->data) != EOF ) /* 21 */ { /* 22 */ head->next = previous; /* 23 */ previous = head; /* 24 */ } /* 25 */ /* 26 */ Output_List(previous); /* 27 */ printf("\n"); /* 28 */ } /* 29 */ /* 30 */ struct Node_type *getmemory(void) /* 31 */ { /* 32 */ return( (struct Node_type *)malloc(sizeof(struct Node_type)) ); /* 33 */ } /* 34 */ /* 35 */ void Output_List(struct Node_type *p) /* 36 */ { /* 37 */ while( p != NULL ) /* 38 */ { /* 39 */ printf("%8d", p->data); /* 40 */ p = p->next; /* 41 */ } /* 42 */ }プログラム7-2-2
/* 1 */ /* Example 7-2-2 */ /* 2 */ /* Making List (Reversal oedre) */ /* 3 */ /* 4 */ #include<stdio.h> /* 5 */ /* 6 */ struct Node_type{ /* 7 */ int data; /* 8 */ struct Node_type *next; /* 9 */ }; /* 10 */ /* 11 */ struct Node_type *getmemory(void); /* 12 */ void Output_List(struct Node_type *p); /* 13 */ /* 14 */ main() /* 15 */ { /* 16 */ struct Node_type *head, *previous; /* 17 */ int n; /* 18 */ /* 19 */ previous = NULL; /* 20 */ /* 21 */ while( scanf("%d", &n) != EOF ) /* 22 */ { /* 23 */ head=getmemory(); /* 24 */ head->data = n; /* 25 */ head->next = previous; /* 26 */ previous = head; /* 27 */ } /* 28 */ /* 29 */ Output_List(head); /* 30 */ printf("\n"); /* 31 */ } /* 32 */ /* 33 */ struct Node_type *getmemory(void) /* 34 */ { /* 35 */ return( (struct Node_type *)malloc(sizeof(struct Node_type)) ); /* 36 */ } /* 37 */ /* 38 */ void Output_List(struct Node_type *p) /* 39 */ { /* 40 */ while( p != NULL ) /* 41 */ { /* 42 */ printf("%8d", p->data); /* 43 */ p = p->next; /* 44 */ } /* 45 */ }解説
-
例7-1では,リストの末尾に新しいノートを加えたが,ここでは,リストの先頭にノードを加える点が異なる.常に新しく確保した領域をheadが指すようになっている.
例7-3 整数値データを入力し、データが昇順に並ぶようにリストを構成せよ。ただし、同じ数値が入力された場合はなにもしない。
考え方
- 入力されたデータを持ってリストを渡って行き、リスト内のデータが入力データよりも大きくなる所まで行く。
- 新しい記憶領域を確保して、入力データを格納し、1.で行き着いた領域の前に、新しい領域を挿入する。
プログラム7-3
/* 1 */ /* Program 7-3 */ /* 2 */ /* Insertion of Data */ /* 3 */ /* 4 */ #include <stdio.h> /* 5 */ /* 6 */ struct node_type{ /* 7 */ int data; /* 8 */ struct node_type *next; /* 9 */ }; /* 10 */ typedef struct node_type NODE; /* 11 */ /* 12 */ NODE *insert( int x, NODE *current ); /* 13 */ /* 14 */ main() /* 15 */ { /* 16 */ int x; /* 17 */ NODE *start, *current; /* 18 */ /* 19 */ start = current = NULL; /* 20 */ while( scanf("%d", &x) != EOF ) /* 21 */ { /* 22 */ start = insert( x, start ); /* 23 */ } /* 24 */ /* 25 */ current = start; /* 26 */ printf("Output Data\n"); /* 27 */ while( current != NULL ) /* 28 */ { /* 29 */ printf("%d \n", current->data ); /* 30 */ current = current->next; /* 31 */ } /* 32 */ } /* 33 */ /* 34 */ NODE *insert( int x, NODE *current ) /* 35 */ { /* 36 */ NODE *p; /* 37 */ /* 38 */ if( current == NULL ) /* 39 */ { /* 40 */ p = (NODE *)malloc(sizeof(NODE)); /* 41 */ p->data = x; /* 42 */ p->next = NULL; /* 43 */ } /* 44 */ else if( current->data < x ) /* 45 */ { /* 46 */ current->next = insert(x, current->next); /* 47 */ p = current; /* 48 */ } /* 49 */ else if( current->data > x ) /* 50 */ { /* 51 */ p = (NODE *)malloc(sizeof(NODE)); /* 52 */ p->data = x; /* 53 */ p->next = current; /* 54 */ } /* 55 */ else /* 56 */ { /* 57 */ p = current; /* 58 */ } /* 59 */ return( p ); /* 60 */ }解説
- 入力されたデータを持ってリストを渡って行き、リスト内のデータが入力データよりも大きくなる所まで行く。
-
関数insert内において,53行目は新しく確保したノードとその次のノードをつなぐ命令である.しかし,新しく確保したノードとその前のノードとをつなぐ明示的な命令は存在していないことに注意すること.関数insertは,59行目で新しく確保したノードの番地を戻しているため,関数を呼び出した命令部(22, 46行目)で新しく確保したノードとその前のノードとをつなぐ操作を行っている.
プログラム7-3を配列を用いて実装した例を以下に示そう.
プログラム7-3-2
/* 1 */ /* Program 7-3-2 */ /* 2 */ /* Insertion of Data (Array type Ver.) */ /* 3 */ /* 4 */ #include <stdio.h> /* 5 */ #define LISTISZE 100 /* 6 */ /* 7 */ struct node_type{ /* 8 */ int data; /* 9 */ int next; /* 10 */ }; /* 11 */ typedef struct node_type NODE; /* 12 */ /* 13 */ NODE list[LISTISZE]; /* 14 */ int maxlist = 0; /* 15 */ /* 16 */ int insert( int x, int current ); /* 17 */ /* 18 */ main() /* 19 */ { /* 20 */ int x, start, current; /* 21 */ /* 22 */ start = current = 0; /* 23 */ while( scanf("%d", &x) != EOF ) /* 24 */ { /* 25 */ start = insert( x, start ); /* 26 */ } /* 27 */ /* 28 */ printf("Output Data\n"); /* 29 */ current = start; /* 30 */ while( current != 0) /* 31 */ { /* 32 */ printf("%d \n", list[current].data ); /* 33 */ current = list[current].next; /* 34 */ } /* 35 */ } /* 36 */ /* 37 */ int insert( int x, int current ) /* 38 */ { /* 39 */ int p; /* 40 */ /* 41 */ if( current == 0 ) /* 42 */ { /* 43 */ p = ++maxlist; /* 44 */ list[p].data = x; /* 45 */ list[p].next = 0; /* 46 */ } /* 47 */ else if( list[current].data < x ) /* 48 */ { /* 49 */ list[current].next = insert(x, list[current].next); /* 50 */ p = current; /* 51 */ } /* 52 */ else if( list[current].data > x ) /* 53 */ { /* 54 */ p = ++maxlist; /* 55 */ list[p].data = x; /* 56 */ list[p].next = current; /* 57 */ } /* 58 */ else /* 59 */ { /* 60 */ p = current; /* 61 */ } /* 62 */ return( p ); /* 63 */ }
基本的な考え方は,プログラム7-3と同様である.配列を用いる場合,あらかじめ必要とする格納領域を確保する(13行目)必要がある.格納位置を示すポインタとして,配列の添え字を用いている.ポインタ型と配列の大きな違いは,格納領域の確保の仕方にある.配列の場合,あらかじめ格納データの量を判断し,プログラム内で宣言された量がコンパイル時に確保される.つまり,配列のためのメモリ領域がプログラム実行前にはすでに存在していることになる.これに対しポインタ型の場合,プログラム内では一つのノードの構成とサイズが定義されているだけで,メモり上にその領域が確保されていない.プログラムの実行中に必要に応じ領域が確保される.そのための命令が,mallocである.
ポインタにより実装されたリストは,データ数が確定していないような対象に対しデータの挿入削除で威力を発揮する.
演習問題
- 例7-3において、 insert を再帰を用いないで実装せよ。
---- ---------- ---------- ---------- ----------
Head | ・-+--→| DATA |・-|--→ | DATA |・-|--→ | DATA |・-|-→ | DATA |/ |
---- ---------- ---------- ---------- ----------
↑ ↑
先頭データ 末尾データ
図に示したように、データが左から右へ一方向に鎖でつながれた構造が線形リストである。図のデータとポインタが格納されている1つ1つの箱をノード(またはセル)と呼び,箱内のデータをノードの構成要素と呼ぶ。ここでデータは実数データ、文字データ、データの組なんでもよい。末尾データの次を指すポインタは、便宜上"/"を埋めておく。これは、次に指すデータが存在しないことを意味する。参考書などでは、"/"を"nil"や"NIL"や"−"で表わすことがあるが、すべて同じ意味である。C言語のプログラムでは"NILL"という特殊記号で表現する。線形リストは一見すると配列とよく似ているが全く違うものである。今、1から10の数値が順に配列とリストにそれぞれ格納されているものとする。

配列の場合、添字の概念とそれにより指定された記憶領域が存在するため、5番目のデータを指定すれば5が即座に得られる。これに対してリストは添字の概念が全くないため、Head から順に5回ポインタを渡って5番目のデータを得ることができる。4と5の間にデータ4.5を挿入することを考えてみよう。配列の場合、10から5までを順に右へ移動し,5が格納されていた場所に4.5を格納することになる。このように、記憶領域そのものを変更することになる。リストの場合、新たに別の記憶領域を確保しそこに4.5を格納し、つぎのデータを指すポインタを5の記憶領域を指すようにする。そして、4の次を指すポインタを4.5の格納領域を指すように変更する。
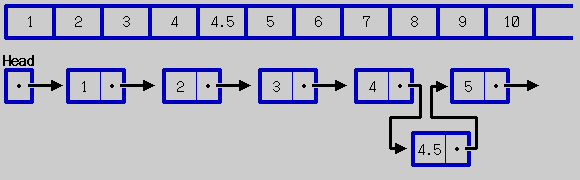
このようにもとのデータの記憶領域は変更せず、新しいデータを挿入することができる。さらに、大きな相違点はリストは抽象的なデータ構造であるため、実装方法は全く規定されていないことである。C言語にはポインタという便利な型があるのでポインタ型を使えばリストが簡単に実装できるが、構造体と配列を組み合わせてリストを実装することもできる。
では、リストをどの様に実装すればよいであろうか? 以下の例によりリストの実装とについて学ぼう。
7.1.2 双方向連結リスト
-
線形リストは左から右へといったように、1方向の結合鎖しかもたないリストであった。現在指しているポインタの1つ前のセルの内容を知りたいとき、わざわざ head から順にたどってこなければならなかった。もし、逆向きの結合鎖を持っていれば効率よく1つ前に情報を得ることができる。これは双方向連結リストで実現できる。
例7-4 入力したデータの順につながった双方向連結リストを作成し,先頭からと後ろから順に格納データを出力せよ.
プログラム7-4
/* 1 */ /* Example 7-4 */ /* 2 */ /* Making List (Double link) */ /* 3 */ /* 4 */ #include<stdio.h> /* 5 */ /* 6 */ struct Node_type{ /* 7 */ int data; /* 8 */ struct Node_type *next; /* 9 */ struct Node_type *back; /* 10 */ }; /* 11 */ /* 12 */ struct Node_type *getmemory(void); /* 13 */ void Output_List(struct Node_type *p); /* 14 */ void Output_List_Rev(struct Node_type *p); /* 15 */ /* 16 */ main() /* 17 */ { /* 18 */ struct Node_type *head, *current, *tail; /* 19 */ int n; /* 20 */ /* 21 */ head = getmemory(); /* 22 */ scanf("%d", &head->data); /* 23 */ tail = head; /* 24 */ head->next = NULL; /* 25 */ head->back = NULL; /* 26 */ /* 27 */ while( current=getmemory(), scanf("%d", ¤t->data) != EOF ) /* 28 */ { /* 29 */ tail->next = current; /* 30 */ current->back = tail; /* 31 */ tail = current; /* 32 */ } /* 33 */ /* 34 */ Output_List(head); /* 35 */ printf("\n"); /* 36 */ /* 37 */ Output_List_Rev(tail); /* 38 */ printf("\n"); /* 39 */ /* 40 */ } /* 41 */ /* 42 */ struct Node_type *getmemory(void) /* 43 */ { /* 44 */ return( (struct Node_type *)malloc(sizeof(struct Node_type)) ); /* 45 */ } /* 46 */ /* 47 */ void Output_List(struct Node_type *p) /* 48 */ { /* 49 */ while( p != NULL ) /* 50 */ { /* 51 */ printf("%8d", p->data); /* 52 */ p = p->next; /* 53 */ } /* 54 */ } /* 55 */ /* 56 */ void Output_List_Rev(struct Node_type *p) /* 57 */ { /* 58 */ while( p != NULL ) /* 59 */ { /* 60 */ printf("%8d", p->data); /* 61 */ p = p->back; /* 62 */ } /* 63 */ } /* 64 */演習問題
-
例7.3と例7.4を参考にして, 整数値データを入力し、データが昇順に並ぶように双方向連結リストを構成せよ。ただし、同じ数値が入力された場合はなにもしない。
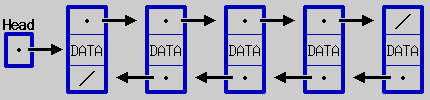
双方向リストは図で示したように、各ノードに前と後ろを指すポインタを導入したリストである。
7.2 木構造
7.2.1 木のに関する基本事項
-
リストは、一方向にポインタがつながれた構造であったが、本節では計算機の分野ではとても重要でかついろいろな場面で応用されている、木構造について解説する。
木の定義
-
上記定義で、T1,...,Tnは、Tの部分木と呼ぶ。(1) ただ一つの頂点からなるデータは木である。 (2) T1,T2,...,Tnがそれぞれ木でありr1,r2,...,rnを それぞれ木の根とする。この時、それぞれの根に向かう辺(r,r1),(r,r2),...,(r,rn)で1つにまとめたデータは木Tであり、頂点rはTの根である。 (3) すべての木は(1)をもとに(2)を有限回繰り返し適用して得られる。 通常我々が目にする木は、下に根があり上方向へ伸びている。計算機分野では便宜上、根を左に右方向へ木が伸びている(もしくは根を上に下方向へ木が伸びている)ように表現する。
+--b | +--d +--a-+--c | +--e r-+ +--h | | +--f----g-+ +--k | +--l +--i-+--j +--mこの例では、すべてのアルファベットは頂点である。rは根であり、a,f,g,iは分岐の頂点、b,d,c,e,h,k,l,j,kは葉である。b,a,fはrの子供の頂点であり同一階層(レベル)にあるという。同様にd,c,eはあの子供の頂点であり、同一の階層である。gはd,c,eと階層の深さは同じであるが、親の頂点が違うため同じ階層にあるとは言えない(階層の深さは同じ)。一般に根は階層0、b,a,fは階層1、d,c,e,gは階層2、h,iは階層3、k,l,j,mは階層4に位置す ると言う。子供たちの頂点間になんらかの順序が定義されている木を順序木と呼ぶ。例えば、d>c>e, b>a>f, h>i, k>l>j>m のように同じ親を持つ子ども達の頂 点に大小関係を持たせると上記木は、順序木となる。さらに、順序木の特別な場合として、1つの頂点はn個以下の部分木をもつような木をn分木と呼ぶ。n=2の場合について検討してみよう。
艨Xが目にする木は、1つの根から上方向にいくつもの枝が伸び、途中から枝別れし、最後には葉がついている。これと同じ構造を計算機内部に表現することにより、あるデータの集まりを階層的に2次元的に表現することができる。このように階層化された構造とそこに格納されているデータを抽象的にとらえたデータ型が木構造である。木構造は、会社の組織、都道府県や市町村のように階層的にデータを分類するようなところで応用される。
木は、グラフ理論に属する分野であり、形式的に取り扱うことがきる。木Tは頂点の集合Vと辺の集合Eの組であり、T=(V,E)と表現される。木の出発点を根(ルート)と呼びrで表現する。当然一つの木には必ず一つだけの根が存在する。頂点x,yを結ぶ辺を(x,y)と表現し、頂点xはyの親、頂点yはxの子供と呼ぶ。木は次のように帰納的に定義される。
7.2.2 2分木の構成
-
2分木とは、各分岐の頂点は必ず2つの部分木を持ち、子ども達の頂点間に順序が定義されている。
例 2分木の例
+---11 +---15-+ | +---18 +---22 20-+ +---25+ | +---30+ +---29 +---40-+ +---33 | | +---49 +---55+ +---61このように、各頂点に整数データが格納されており、部分木+---x y+ +---zに対して、x>y>zの関係が常に成り立っている。2分はデータ検索やデータの並べ換えなどに有効なデータ構造である。次の例では2分木を構成する。2分木といえば、データ間になんらかの関係があることに注意。
例7−5 整数データを読み込んだ順に2分木を構成する。
考え方:
- データの入力。
- もし、目標となる頂点が存在しなければ頂点を作成し、入力データを格納し部分木を構成。
- 目標頂点が存在した場合、入力データと頂点に格納されているデータの大小関係を比べて、入力データの方が小さければ右(上)の頂点へ移動、入力データの方が大きければ左(下)の頂点へ移動。
- 上記1〜3をデータが無くなるまで繰り返す。
/* 1 */ /* Program 7-5 */ /* 2 */ /* Making a Binary Tree */ /* 3 */ /* 4 */ #include <stdio.h> /* 5 */ /* 6 */ struct BinNode_type{ /* 7 */ int data; /* 8 */ struct BinNode_type *left, *right; /* 9 */ }; /* 10 */ typedef struct BinNode_type BinNode; /* 11 */ /* 12 */ BinNode *makenode( int x, BinNode *current ); /* 13 */ BinNode *getmemory(void); /* 14 */ void printnode(BinNode *current, int depth ); /* 15 */ /* 16 */ main() /* 17 */ { /* 18 */ int x, depth; /* 19 */ BinNode *root; /* 20 */ /* 21 */ root = NULL; /* 22 */ while( scanf("%d", &x) != EOF ) /* 23 */ { /* 24 */ root = makenode( x, root ); /* 25 */ } /* 26 */ depth = 0; /* 27 */ printnode( root, depth ); /* 28 */ } /* 29 */ /* 30 */ BinNode *makenode( int x, BinNode *current ) /* 31 */ { /* 32 */ /* 33 */ if( current == NULL ) /* 34 */ { /* 35 */ current = (BinNode *)malloc(sizeof(BinNode)); /* 36 */ current->data = x; /* 37 */ current->left = current->right = NULL; /* 38 */ } /* 39 */ else if( current->data < x ) /* 40 */ { /* 41 */ current->left = makenode(x, current->left); /* 42 */ } /* 43 */ else if( current->data > x ) /* 44 */ { /* 45 */ current->right = makenode(x, current->right); /* 46 */ } /* 47 */ return( current ); /* 48 */ } /* 49 */ /* 50 */ BinNode *getmemory(void) /* 51 */ { /* 52 */ return( (BinNode *)malloc(sizeof(BinNode)) ); /* 53 */ } /* 54 */ /* 55 */ void printnode(BinNode *current, int depth ) /* 56 */ { /* 57 */ int i; /* 58 */ /* 59 */ depth++; /* 60 */ if( current!= NULL ) /* 61 */ { /* 62 */ printnode( current->right, depth ); /* 63 */ for( i=1; i<=depth; i++) printf(" "); /* 64 */ printf("%5d\n", current->data); /* 65 */ printnode( current->left, depth ); /* 66 */ } /* 67 */ depth--; /* 68 */ }実行例
456 78 12 95 65 86 123 654 789 951 753 156 46 58 12 46 58 65 78 86 95 123 156 456 654 753 789 951解説
-
実行例において、縦に並んだ数字列は入力データ、それ以降が実行結果である。456を木の根とし、78,654が階層1のデータ、12,95,789が階層2のデータである。
6〜9: 木の頂点を構造体を用いて表現する。 ┌─┐ │・───→ 右(上)の部分木へのポインタ ├─┤ │デ│ │|│ │タ│ ├─┤ │・───→ 左(下)の部分木へのポインタ └─┘頂点のイメージは図に示したように、2つのポインタと1つのデータ格納領域を持っている。16〜28: メインプログラムで格納するデータの読み込みを行い、2分木に登録する関数を呼び出している。最後に、2分木のイメージを出力する関数を呼んでいる。 30〜47: 2分木を構成するように、既に格納されているデータと新しく格納するデータとの大小関係を調べ、頂点を生成し、ポインタで結ぶ位置の決定とデータの格納を行なう。この関数は再帰的に定義されており、ポインタを伝わって階層を深く潜って行くように書かれている。データの登録が終わると、再帰プログラムを戻ると同時にポインタのアドレスが戻されるため、部分木へのポインタがうまくつながれる。 50〜53: 頂点1つ分の記憶領域を確保するための関数である。構造体BinNodeで宣言した大きさが、動的(実行時)にメモリ上に確保される。 55〜68: 2分木を右から左に順に走査し、入力データを昇順に出力する関数である。変数depthは、階層の深さを表わし出力の際に段付けを行なうために導入した。 演習問題
- 構造体の配列を使って、例7−5を実現せよ。ポインタは、配列の添字の番号で代用する。
7.2.3 2分木によるデータ検索
-
本節では、2分木を用いたデータ検索について考える。
例7−6 検索のキーとなる単語を入力し、その単語が2分木上に存在しているか否かを出力するプログラムを作れ。
実行例1
satou tanaka yamada kaihu murayama miyazawa nakasone satou ozawa uno hata miki hukuda yoshida ishihara hatoyama watanabe suzuki hata hatoyama hukuda ishihara kaihu miki miyazawa murayama nakasone ozawa satou suzuki tanaka uno watanabe yamada yoshida satou exists in this BinTree.実行例2
nagashima tanaka yamada kaihu murayama miyazawa nakasone satou ozawa uno hata miki hukuda yoshida ishihara hatoyama watanabe suzuki hata hatoyama hukuda ishihara kaihu miki miyazawa murayama nakasone ozawa satou suzuki tanaka uno watanabe yamada yoshida nagashima does not exist in this BinTree.解説
-
実行例において、単語列の第1番目が検索するキーデータであり、それ以降が2分木に登録されているデータである。登録されている場合(実行例1)と、されていない場合(実行例2)について行なった。
1〜80: プログラム7−5とほとんど同じである。 82〜95: 2分木内のデータを検索する関数である。もし、同じ単語が見つかれば関数の値は1、見つからなければ値は0となる。考え方は2分木を構成する関数makenodeと同様である。 例7−6の実行例で入力したデータ列において、キーデータとして"suzuki"を入力した場合、入力順に線形リストを作成し検索を行なうと17回の比較を行なって存在を確認できる。これに対し、2分木による検索では、6回の比較で存在の確認ができた。このことからも判るように、2分木による検索は線形リストを用いるよりも効率が良いことが容易にわかるであろう。 しかし、同じ2分木においても葉となる頂点の階層の深さが違うことに注意しよう。"yosida"をキーデータとした場合の比較回数は3回であるのに対し、"suzuku"の場合2倍もかかっている。つまり、2分木は単語の登録順序によりこのような検索の回数が異なるような不都合が生じる。以下の入力データに対するプログラム7−6の実行結果を見てみよう。
yoshida hata hatoyama hukuda ishihara miki murayama nakasone ozawa satou suzuki tanaka uno watanabw yamada yoshida hata hatoyama hukuda ishihara miki murayama nakasone ozawa satou suzuki tanaka uno watanabw yamada yoshida yoshida is exist in this BinTree.一見、2分木が作られていないように見えるが、エラーではない。上記のように意図的にソートされたデータを入力すると左方向へしか伸びない2分木が構成されてしまう。これは特別な場合であるが、入力データの順序(性質)により構成される2分木が異なり、階層の深さが均一な木が構成されなくなる。そこで、最悪のケースでも比較回数が線形リストのように大きくならないような、バランスのとれた2分木を構成したい。 例7−7 階層の深さが均一な2分木を構成するプログラムを作る。
考え方:
- 入力データの個数を調べ、できるだけ頂点からつながる部分木の頂点の総数が、左右で等しくなるようにする。
/* 1 */ /* Program 7-7 */ /* 2 */ /* Making a Balanced Binary Tree */ /* 3 */ /* 4 */ #include <stdio.h> /* 5 */ /* 6 */ struct BinNode_type{ /* 7 */ int data; /* 8 */ struct BinNode_type *left, *right; /* 9 */ }; /* 10 */ typedef struct BinNode_type BinNode; /* 11 */ /* 12 */ BinNode *maketree( int number ); /* 13 */ BinNode *getmemory(void); /* 14 */ void printnode(BinNode *current, int depth ); /* 15 */ /* 16 */ /* 17 */ int counter, x[100]; /* 18 */ /* 19 */ main() /* 20 */ { /* 21 */ int i, number, depth; /* 22 */ BinNode *root; /* 23 */ /* 24 */ i = counter = 0; /* 25 */ while( scanf("%d", &x[i++]) != EOF ); /* 26 */ /* 27 */ root = maketree( i-1 ); /* 28 */ depth = 0; /* 29 */ printnode( root, depth ); /* 30 */ } /* 31 */ /* 32 */ BinNode *maketree( int number ) /* 33 */ { /* 34 */ int lefttree, righttree; /* 35 */ BinNode *p; /* 36 */ /* 37 */ if( number == 0 ) /* 38 */ { /* 39 */ p = NULL; /* 40 */ } /* 41 */ else /* 42 */ { /* 43 */ righttree = number/2; /* 44 */ lefttree = number-righttree-1; /* 45 */ p = (BinNode *)malloc(sizeof(BinNode)); /* 46 */ p->right = maketree( righttree ); /* 47 */ p->data = x[counter++]; /* 48 */ p->left = maketree( lefttree ); /* 49 */ } /* 50 */ /* 51 */ return( p ); /* 52 */ } /* 53 */ /* 54 */ BinNode *getmemory(void) /* 55 */ { /* 56 */ return( (BinNode *)malloc(sizeof(BinNode)) ); /* 57 */ } /* 58 */ /* 59 */ void printnode(BinNode *current, int depth ) /* 60 */ { /* 61 */ int i; /* 62 */ /* 63 */ depth++; /* 64 */ if( current!= NULL ) /* 65 */ { /* 66 */ printnode( current->right, depth ); /* 67 */ for( i=1; i<=depth; i++) printf(" "); /* 68 */ printf("%5d\n", current->data); /* 69 */ printnode( current->left, depth ); /* 70 */ } /* 71 */ depth--; /* 72 */ }実行例
12 46 58 65 78 86 95 123 156 456 654 753 789 951 12 46 58 65 78 86 95 123 156 456 654 753 789 951解説
-
32〜49: バランスのとれた2分木を構成する関数である。データの個数を引数として、データ列の真ん中に位置するデータを、中心の頂点に格納し、その左右のデータ列をそれぞれ左右の部分木とする。左右の部分木についても同様な操作を行なっている。 実行例では、プログラム7−5で用いたデータ(入力順は異なる)を利用した。2分木を構成するため本来ならば、入力されたデータをなんらかの手段で並べ換えをしてその結果を用いて、バランスのとれた2分木を作らなければならない。本プログラムでは、データの並べ換えの部分を省略し、並べ換えが済んでいるデータを入力した。
実行結果からもわかるように、階層の深さが最大でも3であり、プログラム7−5の2分木と比べるとバランスがとれていることがわかる。この2分木を使ったデータ検索では、比較回数は最悪ケースでも4回となる。
第6章で学んだ計算量(O:オーダー)について考えてみる。線形リストは、データの数が多くなればそれに比例して、最悪の場合の比較回数は増す。実際、線形リストによる検索はO(n)(nはデータの数) である。これに対し、バランスのとれた2分木では最悪の場合の比較回数は、極端に多くなることはなく、階層の深さと同じである。階層の深さはデータの数をnとした場合、log_2(n)となる。バランスがとれていない2分木は、最悪の場合線形リストとなるためO(n)であると言えるが、多くの参考書ではO(log_2(n))に近いと説明されている。
さらにバランスのとれた2分木でも、検索回数が頻繁なデータほど浅い階層の所に格納、逆に頻度が少ないデータほど階層の深いところに格納することにより、さらに検索の効率を上げることができる。
今、英単語を辞書で引くことを考えてみよう。コンピュータを使って行なう場合、コンピュータはアルファベットの順序以外何の予備知識を持たないとすると、次の2つの方法が簡単に思いつく。
| 1) | 辞書の先頭から順に引きたい単語と同じ単語が出現するまで1つずつ検索を行なう。 |
| 2) | 辞書の真ん中に位置する単語と引きたい単語を比べ、引きたい単語が真ん中よりも前にあるのか後ろにあるのかを判断する。引きたい単語が存在する半分の辞書に対し、さらにその真ん中の単語と引きたい単語を比べ、引きたい単語が真ん中よりも前にあるのか後ろにあるのかを判断する。以下同様な操作を単語が発見できるまで繰り返す。 |
/* 1 */ /* Program 7-6 */
/* 2 */ /* Search Data */
/* 3 */
/* 4 */ #include <stdio.h>
/* 5 */ #include <string.h>
/* 6 */
/* 7 */ struct BinNode_type{
/* 8 */ char data[20];
/* 9 */ struct BinNode_type *left, *right;
/* 10 */ };
/* 11 */ typedef struct BinNode_type BinNode;
/* 12 */
/* 13 */ BinNode *makenode( char *x, BinNode *current );
/* 14 */ BinNode *getmemory(void);
/* 15 */ void printnode(BinNode *current, int depth );
/* 16 */ int searchdata( BinNode *current, char *key );
/* 17 */
/* 18 */ main()
/* 19 */ {
/* 20 */ char x[20], key[20];
/* 21 */ int depth;
/* 22 */ BinNode *root;
/* 23 */
/* 24 */ scanf("%s", key);
/* 25 */ root = NULL;
/* 26 */ while( scanf("%s", x) != EOF )
/* 27 */ {
/* 28 */ root = makenode( x, root );
/* 29 */ }
/* 30 */ depth = 0;
/* 31 */ printnode( root, depth );
/* 32 */ scanf("%s", key);
/* 33 */ if( searchdata( root, key ) )
/* 34 */ printf("%-20s exists in this BinTree.\n", key);
/* 35 */ else
/* 36 */ printf("%-20s does not exist in this BinTree.\n", key);
/* 37 */ }
/* 38 */
/* 39 */ BinNode *makenode( char *x, BinNode *current )
/* 40 */ {
/* 41 */ if( current == NULL )
/* 42 */ {
/* 43 */ current = (BinNode *)malloc(sizeof(BinNode));
/* 44 */ strcpy( current->data, x );
/* 45 */ current->left = current->right = NULL;
/* 46 */ }
/* 47 */ else if( strcmp(current->data, x) < 0 )
/* 48 */ {
/* 49 */ current->left = makenode(x, current->left);
/* 50 */ }
/* 51 */ else if( strcmp(current->data, x) > 0 )
/* 52 */ {
/* 53 */ current->right = makenode(x, current->right);
/* 54 */ }
/* 55 */ return( current );
/* 56 */ }
/* 57 */
/* 58 */ BinNode *getmemory(void)
/* 59 */ {
/* 60 */ return( (BinNode *)malloc(sizeof(BinNode)) );
/* 61 */ }
/* 62 */
/* 63 */ void printnode(BinNode *current, int depth )
/* 64 */ {
/* 65 */ int i;
/* 66 */
/* 67 */ depth++;
/* 68 */ if( current->right== NULL )
/* 69 */ {
/* 70 */ for( i=1; i<=depth; i++) printf(" ");
/* 71 */ printf("%-20s\n", current->data);
/* 72 */ }
/* 73 */ else
/* 74 */ {
/* 75 */ printnode( current->right, depth );
/* 76 */ for( i=1; i<=depth; i++) printf(" ");
/* 77 */ printf("%-20s\n", current->data);
/* 78 */ }
/* 79 */ if( current->left!=NULL ) printnode( current->left, depth );
/* 80 */ }
/* 81 */
/* 82 */ int searchdata( BinNode *current, char *key )
/* 83 */ {
/* 84 */ int search;
/* 85 */ if( current == NULL )
/* 86 */ search = 0;
/* 87 */ else if( strcmp( current->data, key)==0 )
/* 88 */ search = 1;
/* 89 */ else if( strcmp( current->data, key)<0 )
/* 90 */ search = searchdata( current->left, key );
/* 91 */ else
/* 92 */ search = searchdata( current->right, key );
/* 93 */
/* 94 */ return( search );
/* 95 */ }
7.2.4 2分木の走査
-
2分木の頂点に格納されているデータをどのような順序で参照するかは、扱うデータの性質や処理によって異なる。この参照順序は、以下のような3つに分類できる。例7−7で構成された2分木を例として解説する。
例7−8 2分木を先行順走査してデータを出力せよ。
/* 1 */ /* Program 7-8 */ /* 2 */ /* print data in preorder */ /* 3 */ /* 4 */ #include <stdio.h> /* 5 */ /* 6 */ struct BinNode_type{ /* 7 */ int data; /* 8 */ struct BinNode_type *left, *right; /* 9 */ }; /* 10 */ typedef struct BinNode_type BinNode; /* 11 */ /* 12 */ BinNode *makenode( int x, BinNode *current ); /* 13 */ BinNode *getmemory(void); /* 14 */ void printnode(BinNode *current, int depth ); /* 15 */ void printpreorder(BinNode *current ); /* 16 */ /* 17 */ main() /* 18 */ { /* 19 */ int x, depth; /* 20 */ BinNode *root; /* 21 */ /* 22 */ root = NULL; /* 23 */ while( scanf("%d", &x) != EOF ) /* 24 */ { /* 25 */ root = makenode( x, root ); /* 26 */ } /* 27 */ depth = 0; /* 28 */ printnode( root, depth ); /* 29 */ /* 30 */ printpreorder( root ); /* 31 */ } /* 32 */ /* 33 */ BinNode *makenode( int x, BinNode *current ) /* 34 */ { /* 35 */ /* 36 */ if( current == NULL ) /* 37 */ { /* 38 */ current = (BinNode *)malloc(sizeof(BinNode)); /* 39 */ current->data = x; /* 40 */ current->left = current->right = NULL; /* 41 */ } /* 42 */ else if( current->data < x ) /* 43 */ { /* 44 */ current->left = makenode(x, current->left); /* 45 */ } /* 46 */ else if( current->data > x ) /* 47 */ { /* 48 */ current->right = makenode(x, current->right); /* 49 */ } /* 50 */ return( current ); /* 51 */ } /* 52 */ /* 53 */ BinNode *getmemory(void) /* 54 */ { /* 55 */ return( (BinNode *)malloc(sizeof(BinNode)) ); /* 56 */ } /* 57 */ /* 58 */ void printnode(BinNode *current, int depth ) /* 59 */ { /* 60 */ int i; /* 61 */ /* 62 */ depth++; /* 63 */ if( current!= NULL ) /* 64 */ { /* 65 */ printnode( current->right, depth ); /* 66 */ for( i=1; i<=depth; i++) printf(" "); /* 67 */ printf("%5d\n", current->data); /* 68 */ printnode( current->left, depth ); /* 69 */ } /* 70 */ depth--; /* 71 */ } /* 72 */ /* 73 */ void printpreorder(BinNode *current ) /* 74 */ { /* 75 */ /* 76 */ if( current!= NULL ) /* 77 */ { /* 78 */ printf("%5d\n", current->data); /* 79 */ printpreorder( current->right ); /* 80 */ printpreorder( current->left ); /* 81 */ } /* 82 */ }実行結果
456 78 12 95 65 86 123 654 789 951 753 156 46 58 12 46 58 65 78 86 95 123 156 456 654 753 789 951 456 78 12 65 46 58 95 86 123 156 654 789 753 951演習問題
- 2分木を後行順走査してデータを出力するプログラムを完成させよ。
12
46
58
65
78
86
95
123
156
456
654
753
789
951
| 1) | 先行順走査(preorder)根から走査し、その部分木を右(上)から順に根から走査する。終了しだい、左(下)の部分木を走査する。
|
| 2) | 中順走査(inorder)まず最初に部分木の中で最も深い頂点を走査し、その親の頂点の走査、さらに左(下)の部分木について同様な走査を繰り返す。
|
| 3) | 後行順走査(postorder)左の部分木の奥から子どもの頂点を先に走査し、その親の頂点を走査する。
|
CONTENTS / BACK-PAGE /