Next Sec.: パスの数え上げ
Upper Sec.: グラフに関するアルゴリズム
Prev. Sec.: グラフに関するアルゴリズム
E={(Vi,Vj)}:辺(edge)の有限集合
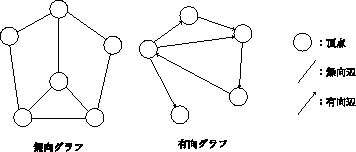
グラフの図形表現

グラフにおける基本概念

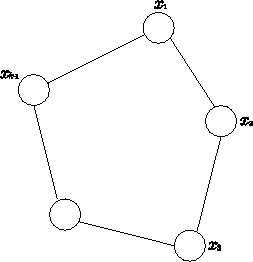
x1からxkへのパス
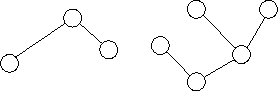

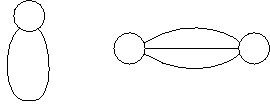
以下の仮定
計算機におけるグラフの表現
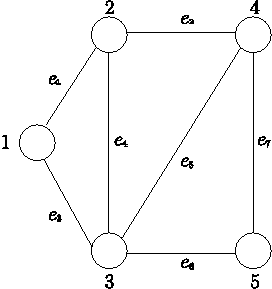
A = (aij)
1 (i,j) in E
aij =
0 otherwise
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 1 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 0 | 1 |
| 5 | 0 | 0 | 1 | 1 | 0 |
B = (bij)
1 i in ej
bij =
0 otherwise
| e1 | e2 | e3 | e4 | e5 | e6 | e7 | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
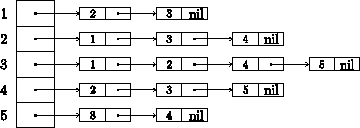
参考:隣接リストの配列表現
| 1 | 2 | 3 | 0 | 0 | 0 |
|---|---|---|---|---|---|
| 2 | 1 | 3 | 4 | 0 | 0 |
| 3 | 1 | 2 | 4 | 5 | 0 |
| 4 | 2 | 3 | 5 | 0 | 0 |
| 5 | 3 | 4 | 0 | 0 | 0 |