Next Sec.: ソーティング Upper Sec.: グラフに関するアルゴリズム Prev. Sec.: パスの数え上げ

最短路問題

「各辺に長さをもつグラフにおいて，１つの頂点sから他のすべての頂点へ の最短路のパスを求めよ．」

ラベリング法の原理


各頂点に，それまで得られたsからのパスの長さとそのパス上の直前の 頂点を示すラベル（label）を与えておき，探索の過程でより短いパスが 見つかった都度それらのラベルを書き換える．

G = (V,E)

与えられたグラフ

d(x,y)

辺(x,y)の長さ

LR[x]

頂点xの経路ラベル（現在までに見いだされた s --> xのパス上におけるxの直前の頂点）

LD[x]

頂点xの距離ラベル（現在までに見いだされた s --> xのパスの長さ）

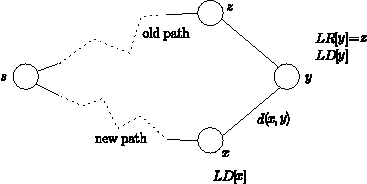
      LD[x]+d(x,y) < LD[y]
           -- > LD[y] := LD[x] + d(x,y) 
                   LR[y] := x

Dijkstraのアルゴリズム
ラベリング法の一種．基本的には頂点の横型検索を行うが，候補頂点の選択順序を距離ラベルの小さい順とする．候補頂点の集合をQLISTとする．即ち，

QLIST:

ラベルの変更を受け，再度チェックする必要のある頂点の集合

以下のアルゴリズムの記述はPASCAL-like

     for all (x in V) do LR[x]:= 0;
     for all (x in V) do LD[x]:= unlimited;
     LD[s] := 0;
     QLIST := {s};
     while QLIST != empty do
     begin
          choose x in QLIST s.t. LD[x] is minimal;
          QLIST := QLIST - {x};
          for each y s.t. ((x,y) in E) and y != LR[x] do
               if LD[x] + d(x,y) < LD[y] then
                    begin
                         LD[y] := LD[x] + d(x,y);
                         LR[y] := x;
                         QLIST := QLIST or {y};
                    end
     end;

このアルゴリズムの結果得られる最短路の記述LRはグラフGのsの 根（root）とする１つの展張木を与える．