第4回　11月18日

電場の導入

原点に点電荷q ，位置 r に点電荷 q’ が静止しているとする．このとき，点電荷q’ の受けるCoulomb力

　 (4.1)

を，次のように２つに分けて考える．

　 (4.2)

および

(4.3）

このように分けて考えることに，何のメリットがあるのだろうか？

(4.3)は「点電荷q によって，E というものが作り出されている」と主張している．

E を，電場という．電場という言葉を用いると，(4.3)式は

「電荷は，電場を作り出す．その大きさは，電荷に比例する」

ということを語っているのである．

また，(4.2)は，

「電場Eの中にある電荷q’ は，電場の向きに力をうけ，その大きさは電荷と電場の大きさに比例する」

ということを意味していることになる．

上のCoulomb力の「分割」を，作為的に感じる人もいるかと思うが，このような発想の転換こそ，自然哲学としての物理の面目躍如たるものがあると思う．つまり，電場の導入によって，たとえ力を及ぼす相手の電荷がなくても「電荷が1個あれば空間には電場というものが生じていて，いつでも他の電荷q’にF=q’E なる力を及ぼす性質を空間がもつようになる」と考えるわけである．

（静電場の段階では分かりづらいが）電場は電磁波のように電荷から切り離されても存在するので，実在と考えてよい．

たくさんの電荷がつくる電場

電荷q_i が位置 r_i にあるとする．この電荷が位置 r につくる電場をE_i とすると，(4.3)式より

(4.4)

である．もし，空間にN個の電荷がある(ただし静止している) とすると，これらの電荷全体が位置r につくる電場は，

(4.5)

という，足し合わせで求まる．この式は，Coulomb力に戻って考えるとすぐに理解できる．

位置rに電荷q’ があるとすると，力はベクトルとして合成されることから

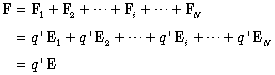
が成立する．よって，(4.5)式が成立する．

(4.4) 式を(4.5)式に代入して，

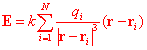(4.6)

を得る．この式によって，原理的にはどのような静電場でも計算できる．ただし，特別な場合を除いて，一般的にはコンピュータが必要である．

電荷分布が連続的な場合は，その連続的な分布を点とみなせる位に小さい領域に分割して考える．そのように考えれば，(4.6)式をあてはめることができる．

点電荷とみなしたi 番目の微小領域は，そこの電荷密度をとして，電荷密度は場所場所で異なってもよいが，微小領域内では一定とみなす．（というより，領域内においては電荷密度が一定とみなせるくらい微小な領域に分割する．)微小領域の体積をΔV とすると，

と表せる．（電荷=電荷密度×体積） これを(4.6)式に代入して，

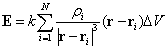
限りなく微小領域を小さくした極限では（N→∞，ΔV→0 ），和は空間積分になって

(4.7)

となる．（ただし，である．）

ときどき積分を見ると目を回す人がいるが，(4.7)式と(4.6)式は実質的に全く同じ式ととらえる感覚が大切である．物理において積分はたくさんの量を足し合わせるという意味を持つに過ぎない．足し合わせの対象を連続量と見るときは積分，とびとびの量と見るときは和（シグマ）で表現しているだけである．

問1：授業では直線上に一様に分布した電荷のつくる電場を求めた．これをノートを見ないで自分で求めてみよ．

問2：半径Rの球内に電荷が一様に分布している．このときの電場を求めよ．総電荷をQとする．