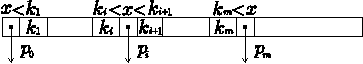Next Sec.: ハッシング（Hashing） Upper Sec.: B木とハッシング Prev. Sec.: 大規模ファイルへのアクセス

B木

２分探索木の拡張

多分木（multiway tree）化とバランス化

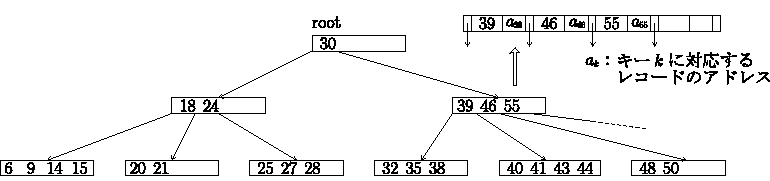
B木（B-tree）の条件

1. 各ノードの型

   キー・エリア 2n 個

   ポインタ・エリア 2n+1 個

2. 各ノードのキーの実装個数

   root ノード 1〜2n 個

   root ノード以外 n〜2n 個

3. キーの格納順序

   個々のノード内 昇順

   気を中順検索した時のキーの出現順序 昇順

a) キーxの探索

探索が下図のようなノードまで進んだとき
x = k_i なら 探索終了
k_i < x < k_i+1 なら ポインタp_iをたどって更に検索
x < k₁ なら ポインタp₀をたどって更に検索
k_m < x なら ポインタp_mをたどって更に検索

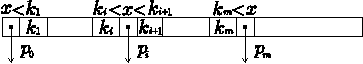
b)

キーxの挿入
xが新しいキーのとき挿入（新しいキーと判断するのは，いずれかのleafノードを探索したとき）

1. そのleafノードに空きがあるとき
   そのノードにxを挿入
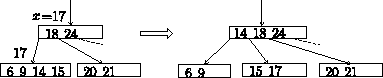
2. そのleafノードに空きがないとき
   下図のようにそのleafノードを分割してxを挿入． 親ノードも修正し，バランスをとる． 親ノードもあふれたときは，この操作を上に伝播

c)

キーxの削除
xをそのノードから削除したのち， xがleafノードにあったか否かによって次のよう処置を行う．

1. xがleafノードにあったとき
   キーの個数 <n（アンダフロー）
   隣接leafノードと合体（必要なら再分割）
   キーの個数 >= n
   そのまま
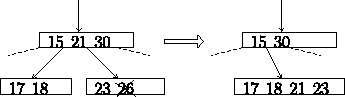
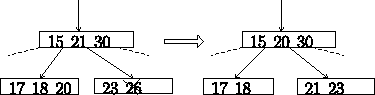
2. xがleaf以外のノードにあったとき
   xに隣接したキー（leafノードにある）を，xのあった位置に移す． 必要なら，そのleafノードのアンダフロー処理を行う．

B木の特徴

1. 各ノードのキーの実装個数が n 〜 2n であり，平均してバランスがとれている．
2. 記憶領域の利用効率は50%以上である．
3. leafノードはすべて同一レベルになる．
4. キーへのアクセスは最悪でも log_n N（Nはキーの総数）回のノード探索ですむ．
5. キーの挿入や削除が動的に起こるような応用に適している．

B木はファイルへのアクセスのみならず言語プロセサなど情報処理の色々な分野で用いられる．