Next Sec.: About this document Upper Sec.: B木とハッシング Prev. Sec.: B木

ハッシング（Hashing）

ハッシングの考え方

与えられた各キーkに対して，そのレコードの格納アドレスをkの関数として計算によって求める方法で，キー変換ともいう．これは，連想メモリを計算によってシミュレートする方法と考えることもできる．

K ----> A = f(k)

Kに対応するレコード・アドレス
f:ハッシュ関数

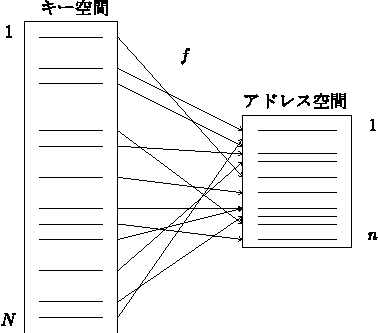
• 一般にキー空間はアドレス空間に比して極めて大

  N >> n

• アドレス空間での衝突（collision）は避けられない

  k₁ != k₂, f(k₁) = f(k₂)

基本的な問題は次の２つ

• ハッシュ関数fの選択
• 衝突が生じたときの処理方法

ハッシュ関数の条件

1. f(k) がアドレス空間の中で，できるだけ一様に分布すること
2. f(k) の計算が簡単で時間を要しないこと

ハッシュ関数の例

1. 合同法（除算法）

   f(K) = K mod n

   0 <= f(K) < n-1

   ただし，nは素数（実用上は，十分大きな素数の積）

   K = 134075

   f(K) = 134075 mod 293 = 174

2. 平方抽出法（Middle of Square）

   f(K) = EXTR_r(K)

   n = 2^r

   ただし，EXTR_rは中位のrビットを抽出することを示す．

   K = 134075 * 134075 17976103625

   f(K) = 610

3. 重ね合わせ法（Folding）

   kを数字列としてこれをいくつかに分け， それらを加えたものを f(K) とする．

   K=134075

   f(K) = 13+40+75 = 128

処理の衝突

衝突（collision）


K₁ != K₂ , f(K₁) = f(K₂)
K₁ , K₂ : シノニム（synonim）

衝突の処理法

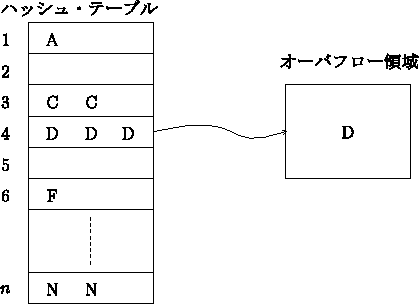
1. パケット法
   各ハッシュ・アドレス対応に数個のシノニムを格納するパケットを用意する． パケットをあふれたシノニムのためにオーバフロー領域が必要である．
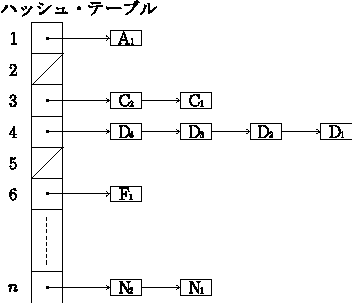
2. 直接チェイニング
   各ハッシュ・アドレスに対応するシノニムをポインタでチェイニングする． ハッシュ・テーブルにはそれらのチェインの先頭を示すポインタを格納
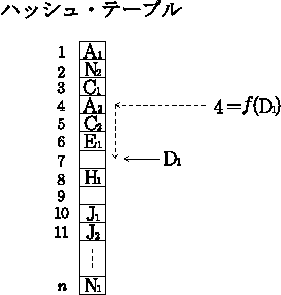
3. オープン・アドレッシング
   ハッシュ・テーブルの各ハッシュ・アドレスには，キーを一個だけ直接格納する． あるキーをハッシュしたとき， そのアドレスにはすでに他のキーが格納されていた場合は， 一定のルールで他のあいているアドレスを見つけ，そこに格納する． キーを探索する場合も同様の手順に従う．
   1. 線形検査法（linear probing）
      アドレスの大きい方へ順番にアドレスを検査していく． 最後のアドレスは最初のアドレスに隣接していると考える．
   2. ２次検査法（quadratic probing）
      バラツキを増すために，最初１つ隣，次は４つ隣， 次は９つ隣というように， 一般に i (i=1,2,3,....)の間隔で検査する．ただし， 上と同様最後のアドレスは最初のアドレスに隣接していると考える．