回帰分析にもとづく予測値と実測値との差、すなわち残差 e_iの平方和 Se が最小になるように回帰母数 ａ とb を定める方法を最小二乗法という。

残差とは　>>

「誤差 ε_iが互いに独立に、平均0、分散σ² の正規分布に従う（不遍性、等分散性、無相関性、正規性）」という条件が満たされる場合は最小二乗法による推定量がよい推定量となる。（条件が変われば，残差の絶対値を最小にすることがよい推定量を与えることがある）

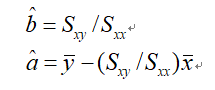
のとき、

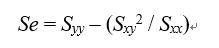
が最小になる。

推定したb^{^} の確かさは信頼区間で示される。100(1–α)％信頼区間 b^{^}±ξは次式で与えられる。

ここでt(φ, α) は自由度φ(= n–2)、有意水準αのt分布の値である。

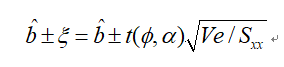
は標準誤差と呼ばれる。 Ve は次式で定義され、誤差分散σ² の不偏推定量である。

標準誤差とは　>>

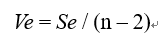
Ｑ　標準誤差は寄与率r²とb^{^} で表すことができる。確かめよ。